
| CA |
| BD |
| CD |
| CA |
| AB |
| BD |
| CD |
| AB |
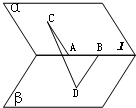 解:如图,
解:如图,| CA |
| BD |
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| BD |
| 1 |
| 2 |
| CD |
| 17 |
| CD |
| AB |
| CA |
| AB |
| BD |
| AB |
| AB |
| CD |
| AB |
| ||||
|
|
| 4 | ||
|
| 2 |
| 17 |
| 17 |
| CD |
| AB |
| 2 |
| 17 |
| 17 |
| 2 |
| 17 |
| 17 |


科目:高中数学 来源: 题型:
 (2013•镇江二模)如图所示,有两条道路OM与ON,∠MON=60°,现要铺设三条下水管道OA,OB,AB(其中A,B分别在OM,ON上),若下水管道的总长度为3km,设OA=a(km),OB=b(km).
(2013•镇江二模)如图所示,有两条道路OM与ON,∠MON=60°,现要铺设三条下水管道OA,OB,AB(其中A,B分别在OM,ON上),若下水管道的总长度为3km,设OA=a(km),OB=b(km).
| ||
| 4 |
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•临沂二模)某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(2013•临沂二模)某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区二模文)(14分)
如图,正△ABC的中线AF与中位线DE相交于点G,![]() 已知△A′DE是△AED绕边DE旋转过程中的一个图形。
已知△A′DE是△AED绕边DE旋转过程中的一个图形。
(I)求证点A′在平面ABC上的射影在线段AF上;
(II)当二面角A′―DE―A为60°时,求三棱锥A′―FED的体积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com