
【题目】为了改善空气质量,某市规定,从2018年1月1日起,对二氧化碳排放量超过![]() 的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下:(单位:
的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下:(单位:![]() )
)
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为![]() .
.
(1)求表中![]() 的值,并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性;
的值,并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌汽车中随机抽取2辆,求至少有1辆二氧化碳排放量超过![]() 的概率.(注:方差
的概率.(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数).
的平均数).
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:
【题目】中国古代数学名草《周髀算经》曾记载有“勾股各自乘,并而开方除之”,用符号表示为![]() ,我们把a,b,c叫做勾股数.下列给出几组勾股数:3,4,5;5,12,13;7,24,25;9,40,41,以此类推,可猜测第5组股数的三个数依次是________.
,我们把a,b,c叫做勾股数.下列给出几组勾股数:3,4,5;5,12,13;7,24,25;9,40,41,以此类推,可猜测第5组股数的三个数依次是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
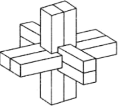
【题目】鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.从外观上看,是严丝合缝的十字立方体,其上下、左右、前后完全对称;六根等长的正四棱柱分成三组,经90°榫卯起来.如图所示,正四棱柱的高为8,底面正方形的边长为1,将这个鲁班锁放进一个球形容器内,则该球形容器半径的最小值为(容器壁的厚度忽略不计)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x-![]() (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+![]() )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有![]() 成立;
成立;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,已知asinB=bsin2A.
(1)求角A;
(2)若a=5,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com