【题目】中国古代数学名草《周髀算经》曾记载有“勾股各自乘，并而开方除之”，用符号表示为
，我们把a，b，c叫做勾股数.下列给出几组勾股数:3，4，5；5，12，13；7，24，25；9，40，41，以此类推，可猜测第5组股数的三个数依次是________.
黄冈冠军课课练系列答案科目：高中数学 来源： 题型：
【题目】[选修4―4：坐标系与参数方程]
在直角坐标系xOy中，直线l1的参数方程为
（t为参数），直线l2的参数方程为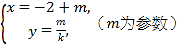
.设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．
（1）写出C的普通方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ(cosθ+sinθ) 
=0，M为l3与C的交点，求M的极径.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（已知数列{
}满足：
，
为数列
的前
项和．
（1） 若{}是递增数列，且
成等差数列，求
的值；
（2） 若
，且{
}是递增数列，{
}是递减数列，求数列{}的通项公式；
（3） 若
，对于给定的正整数，是否存在一个满足条件的数列，使得
，如果存在，给出一个满足条件的数列，如果不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面四边形ABCD中， AB＝2，BD＝
，AB⊥BC，∠BCD＝2∠ABD，△ABD的面积为2．
(1)求AD的长；
(2)求△CBD的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四个命题：
函数
的最大值为1；
“
，
”的否定是“
”；
若
为锐角三角形，则有
；
“
”是“函数
在区间
内单调递增”的充分必要条件．
其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了改善空气质量，某市规定，从2018年1月1日起，对二氧化碳排放量超过
的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下:（单位:
）
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为
.
（1）求表中
的值，并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性；
（2）从被检测的5辆甲品牌汽车中随机抽取2辆，求至少有1辆二氧化碳排放量超过的概率.（注:方差
，其中
为
的平均数）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
