
【题目】已知函数![]() (
(![]() ,
,![]() 为常数)在
为常数)在![]() 内有两极值点
内有两极值点![]()
(1)求实数a的取值范围;
(2)求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,PA![]() 平面ABCD,EB//PA,AB=PA=4,EB=2,F为PD的中点.
平面ABCD,EB//PA,AB=PA=4,EB=2,F为PD的中点.
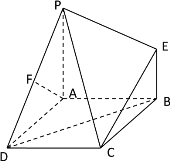
(1)求证AF![]() PC
PC
(2)BD//平面PEC
(3)求二面角D-PC-E的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名草《周髀算经》曾记载有“勾股各自乘,并而开方除之”,用符号表示为![]() ,我们把a,b,c叫做勾股数.下列给出几组勾股数:3,4,5;5,12,13;7,24,25;9,40,41,以此类推,可猜测第5组股数的三个数依次是________.
,我们把a,b,c叫做勾股数.下列给出几组勾股数:3,4,5;5,12,13;7,24,25;9,40,41,以此类推,可猜测第5组股数的三个数依次是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,若关于
时,若关于![]() 的方程
的方程![]() 有唯一实数解,试求实数
有唯一实数解,试求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且不等式
,且不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至2018年底,我国发明专利申请量已经连续8年位居世界首位,下表是我国2012年至2018年发明专利申请量以及相关数据.
总计 | ||||||||
年代代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
申请量 | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
注:年代代码1~7分别表示2012~2018.
(1)可以看出申请量每年都在增加,请问这几年中那一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x-![]() (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+![]() )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有![]() 成立;
成立;
(3)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com