
分析 可作作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,根据条件可以得出OA=2,OB=$\sqrt{6}$,AC⊥BC,从而说明点C在以AB为直径的圆上,从而当OC过圆心时,OC最长,即|$\overrightarrow{c}$|最大,设圆心为D,从而根据OC=OD+DC,由中线长定理,便可得出最大值.
解答 解:如图,作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{a}$-$\overrightarrow{c}$=$\overrightarrow{CA}$,$\overrightarrow{b}$-$\overrightarrow{c}$=$\overrightarrow{CB}$,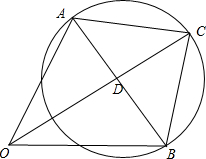
∵($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,
∴$\overrightarrow{CA}$⊥$\overrightarrow{CB}$,
∴AC⊥BC,
∴点C在以AB为直径的圆上,设圆心为D,D为AB中点;
由AB=2;
∴圆半径为1;
∴当OC过D点时,OC最大,即|$\overrightarrow{c}$|最大,
由OD为中点,由中线长定理,可得
(2OD)2+AB2=2(OA2+OB2),
即有4OD2+22=2[22+($\sqrt{6}$)2],
解得OD=2,
则OC的最大值为2+1=3.
故答案为:3.
点评 本题考查数量积的计算公式,向量夹角的概念,用有线向量表示向量,以及向量垂直的充要条件,直径所对的圆周角为直角,数形结合解题的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (理)已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点$(2,\sqrt{2})$.
(理)已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点$(2,\sqrt{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx•sng(x)=sin|x|. | B. | sinx•sng(x)=|sinx| | C. | |sinx|•sng(x)=sin|x| | D. | sin|x|•sng(x)=|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 219-1 | B. | 221-2 | C. | 219+1 | D. | 221+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$,$\frac{5}{3}$] | B. | [-1,$\frac{5}{3}$] | C. | [-3,1] | D. | [$\frac{1}{3}$,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com