
(本小题共13分)已知圆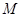 过两点
过两点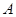 (1,-1),
(1,-1),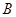 (-1,1),且圆心
(-1,1),且圆心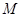 在
在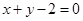 上.
上.
(1)求圆 的方程;
的方程;
(2)设 是直线
是直线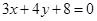 上的动点,
上的动点,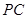 、
、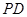 是圆
是圆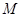 的两条切线,
的两条切线,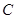 、
、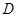 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值.
(1)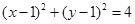 (2)
(2)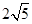
解析试题分析:(1)法一:
线段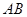 的中点为(0,0),其垂直平分线方程为
的中点为(0,0),其垂直平分线方程为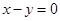 . …2分
. …2分
解方程组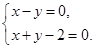 所以圆
所以圆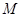 的圆心坐标为(1,1). …4分
的圆心坐标为(1,1). …4分
故所求圆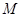 的方程为:
的方程为: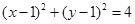 . …6分
. …6分
法二:设圆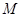 的方程为:
的方程为: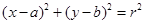 ,
,
根据题意得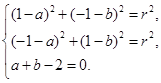 …2分
…2分
解得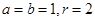 . …4分
. …4分
故所求圆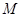 的方程为:
的方程为: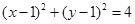 . …6分
. …6分
(2)由题知,四边形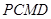 的面积为
的面积为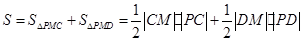 . …8分
. …8分
又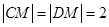 ,
,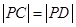 ,
,
所以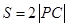 ,而
,而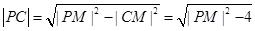 , …10分
, …10分
即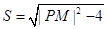 . …11分
. …11分
因此要求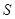 的最小值,只需求
的最小值,只需求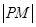 的最小值即可,
的最小值即可,
即在直线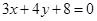 上找一点
上找一点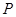 ,使得
,使得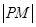 的值最小,
的值最小,
所以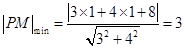 , …12分
, …12分
所以四边形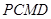 面积的最小值为
面积的最小值为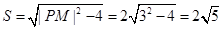 . …13分
. …13分
考点:本小题主要考查圆的标准方程的求法、直线与圆的位置关系的判断和应用,考查学生分析问题、解决问题的能力和运算求解能力.
点评:求解直线与圆的位置关系时,要注意数形结合,可以简化运算,还要注意适当转化.直线和圆所涉及到的知识是整个解析几何的基础,并渗透到解析几何的各个部分,但一般难度不大.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
(本小题共13分)
已知函数![]() 的反函数为
的反函数为![]() ,数列
,数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,
函数![]() 的图象在点
的图象在点![]() 处的切线在
处的切线在![]() 轴上的截距为
轴上的截距为![]() .
.
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)若数列![]() 的项仅
的项仅![]() 最小,求
最小,求![]() 的取值范围;
的取值范围;
(3)令函数![]() ,数列
,数列![]() 满足:
满足:![]() ,且
,且
![]() ,其中
,其中![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三下学期期中考试数学理卷 题型:解答题
(本小题共13分)
已知每项均是正整数的数列 :
: ,其中等于
,其中等于 的项有
的项有 个
个 ,
,
设
 ,
,
 .
.
(Ⅰ)设数列 ,求
,求 ;
;
(Ⅱ)若数列 满足
满足 ,求函数
,求函数 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市丰台区高三下学期统一练习数学理卷 题型:解答题
(本小题共13分)
已知函数 ,
, 为函数
为函数 的导函数.
的导函数.
(Ⅰ)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是 ,求
,求 的值;
的值;
(Ⅱ)若函数 ,求函数
,求函数 的单调区间.
的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com