
已知函数 ,
,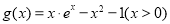 ,且
,且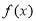 点
点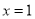 处取得极值.
处取得极值.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若关于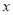 的方程
的方程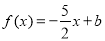 在区间
在区间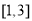 上有解,求
上有解,求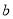 的取值范围;
的取值范围;
(Ⅲ)证明: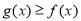 .
.
(1)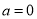 ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)求导,利用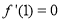 求
求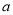 值;(2)分离常数,构造函数,转化为求函数的值域问题;(3)作差构造函数,将证明不等式恒成立问题转化为求函数的最值问题.
值;(2)分离常数,构造函数,转化为求函数的值域问题;(3)作差构造函数,将证明不等式恒成立问题转化为求函数的最值问题.
解题思路: (1)求函数最值的步骤:①求导函数;②求极值;③比较极值与端点值,得出最值;
(2)若函数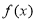 在某区间上单调递增,则
在某区间上单调递增,则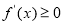 在该区间恒成立;“若函数
在该区间恒成立;“若函数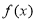 在某区间上单调递减,则
在某区间上单调递减,则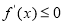 在该区间恒成立.
在该区间恒成立.
试题解析:(Ⅰ)∵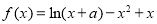 , ∴
, ∴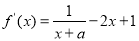
∵函数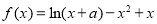 在点
在点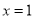 处取得极值,
处取得极值,
∴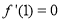 ,即当
,即当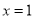 时
时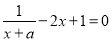 ,
,
∴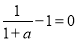 ,则得
,则得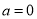 .经检验符合题意 5分
.经检验符合题意 5分
(Ⅱ)∵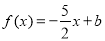 ,∴
,∴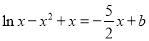 ,
,
∴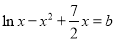 .
.
令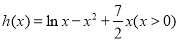 , 6分
, 6分
则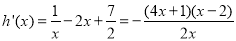 .
.
∴当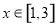 时,
时, 随
随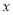 的变化情况表:
的变化情况表:
| 1 | (1,2) | 2 | (2,3) | 3 |
| + | 0 | - | ||
| ↗ | 极大值 | ↘ |
计算得: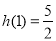 ,
,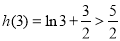 ,
, ,
,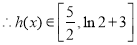
所以 的取值范围为
的取值范围为 。 10分
。 10分
(Ⅲ)证明:令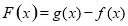
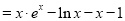
 ,
,
则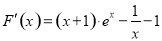
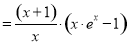 , 11分
, 11分
令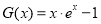 ,则
,则  ,
,
 函数
函数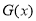 在
在 递增,
递增,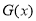 在
在 上的零点最多一个 12分
上的零点最多一个 12分
又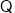
 ,
,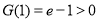 ,
,
 存在唯一的
存在唯一的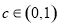 使得
使得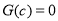 , 13分
, 13分
且当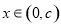 时,
时, ;当
;当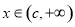 时,
时,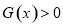 .
.
即当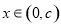 时,
时,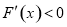 ;当
;当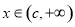 时,
时,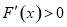 .
.

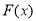 在
在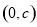 递减,在
递减,在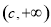 递增,
递增,
从而
 . 14分
. 14分
由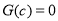 得
得 即
即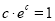 ,两边取对数得:
,两边取对数得: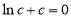 ,
,
 ,
,

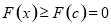 ,
,
从而证得 .
.
考点:1.函数的极值与最值;2.导数的应用;3.函数的单调性.


科目:高中数学 来源: 题型:
 已知一个水平放置的平面图的斜二测直观图是一个平行四边形A′B′C′D′(如图示),其底角为∠D′A′B′=45°,A′B′=2,A′D′=4,则平面图形的实际面积为( )
已知一个水平放置的平面图的斜二测直观图是一个平行四边形A′B′C′D′(如图示),其底角为∠D′A′B′=45°,A′B′=2,A′D′=4,则平面图形的实际面积为( )| A、4 | ||
B、4
| ||
| C、8 | ||
| D、16 |
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考文科数学试卷(解析版) 题型:选择题
过双曲线 的右焦点F2的一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长
的右焦点F2的一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长
为( )
A.18 B. C.
C.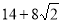 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考理科数学试卷(解析版) 题型:填空题
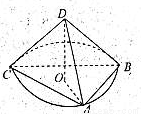
已知四面体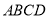 中,
中, ,且
,且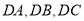 两两互相垂直,点
两两互相垂直,点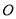 是
是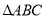 的中心,将
的中心,将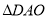 绕直线
绕直线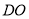 旋转一周,则在旋转过程中,直线
旋转一周,则在旋转过程中,直线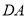 与直线
与直线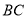 所成角的余弦值的最大值是___ _
所成角的余弦值的最大值是___ _
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考理科数学试卷(解析版) 题型:选择题
如图,椭圆的中心在坐标原点,焦点在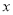 轴上,
轴上,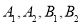 为椭圆顶点,
为椭圆顶点,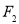 为右焦点,延长
为右焦点,延长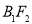 与
与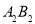 交于点
交于点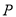 ,若
,若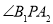 为钝角,则该椭圆离心率的取值范围是( )
为钝角,则该椭圆离心率的取值范围是( )

(A)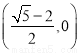 (B)
(B)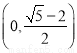
(C)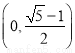 (D)
(D)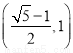
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-3 8.4列联表独立性分析案例练习卷(解析版) 题型:?????
(2013•宜宾一模)在4次独立重复试验中,随机事件A恰好发生一次的概率不小于其恰好发生两次的概率,则事件A在一次试验中发生的概率p的取值范围是( )
A.[0.4,1) B.(0,0.6] C.(0,0.4] D.[0.6,1)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-1 3.9共面与平行练习卷(解析版) 题型:?????
若直线l的方向向量为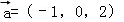 ,平面α的法向量为
,平面α的法向量为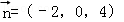 ,则( )
,则( )
A.l∥α B.l⊥α C.l?α D.l与α斜交
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com