Question

【题目】如图，在四棱锥中，底面是矩形，平面平面，，是的中点，，.

（1）求证：；

（2）若二面角的正弦值为，求四棱锥的体积.

Answer 1

【答案】（1）见解析（2）

【解析】分析：（1）由几何关系可证得直线，，两两垂直.以为坐标原点，，，所在直线分别为轴，轴，轴建立空间直角坐标系，设.由空间向量的结论可证得，则.

（2）由（1）可得，.由空间向量计算可得.则四棱锥的体积.

详解：（1）设的中点为，连接，由四边形是矩形，得.

∵，是的中点，∴.

∵平面平面，平面平面，

∴平面. ∴. ∴直线，，两两垂直.

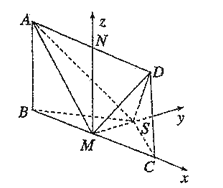
以为坐标原点，，，所在直线分别为轴，轴，轴建立如图所示的空间直角坐标系，设.

依题意得，，，，，，.

∴，.∵，

∴，即.

（2）由（1）可得，.

设平面的法向量为，则，，

∴即

令，则是平面的一个法向量，同理可得是平面的一个法向量.设二面角的大小为，

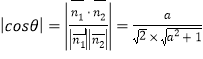则. ∴，解得.

∴四棱锥的体积.