
【题目】已知椭圆C: ![]() =1(a>b>0)的长轴长为4,离心率为
=1(a>b>0)的长轴长为4,离心率为 ![]() ,右焦点为F.
,右焦点为F.
(1)求椭圆C的方程;
(2)直线l与椭圆C相切于点P(不为椭圆C的左、右顶点),直线l与直线x=2交于点A,直线l与直线x=﹣2交于点B,请问∠AFB是否为定值?若不是,请说明理由;若是,请证明.
【答案】
(1)解:2a=4,即a=2,e= ![]() =
= ![]() ,
,
∴c= ![]() ,
,
b= ![]() =1,
=1,
∴椭圆方程为: ![]() ,
,
(2)解:证明:当l的斜率为0时,∠AFB为直角,则∠AFB为定值,为 ![]() ,
,
当斜率不为0时,设切点为P(x0,y0),则l: ![]() ,
,
∴A(2, ![]() ),B(﹣2,
),B(﹣2, ![]() ),
),
∴kAFkBF= 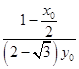
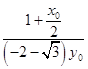 =
= ![]() =﹣1,
=﹣1,
∴∠AFB为定值 ![]()
【解析】(1)由2a=4,离心率e= ![]() =
= ![]() ,b=
,b= ![]() 即可求得a和b,即可求得椭圆C的方程;(2)l的斜率为0时,∠AFB为直角,则∠AFB为定值
即可求得a和b,即可求得椭圆C的方程;(2)l的斜率为0时,∠AFB为直角,则∠AFB为定值 ![]() ,当斜率不为0时,将切点代入椭圆方程,求得交点坐标,求得AF和BF的斜率kAF及kBF , 即可求得kAFkBF=﹣1,即可求得∠AFB为定值
,当斜率不为0时,将切点代入椭圆方程,求得交点坐标,求得AF和BF的斜率kAF及kBF , 即可求得kAFkBF=﹣1,即可求得∠AFB为定值 ![]() .
.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别是a,b,c且满足(2a﹣c)cosB=bcosC.
(1)求角B的大小;
(2)若△ABC的面积为 ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为 ![]() .
. 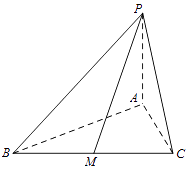
(1)求三棱锥P﹣ABC的体积;
(2)若M是BC的中点,求异面直线PM与AB所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
A.(0, ![]() ]
]
B.(一∞, ![]() ]
]
C.(0, ![]() )
)
D.(一∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(a1 , a2),
=(a1 , a2), ![]() =(b1 , b2),定义一种向量运算
=(b1 , b2),定义一种向量运算 ![]()
![]() =(a1b1 , a2b2),已知向量
=(a1b1 , a2b2),已知向量 ![]() =(2,
=(2, ![]() ),
), ![]() =(
=( ![]() ,0),点P(x′,y′)在y=sinx的图象上运动.点Q(x,y)是函数y=f(x)图象上的动点,且满足
,0),点P(x′,y′)在y=sinx的图象上运动.点Q(x,y)是函数y=f(x)图象上的动点,且满足 ![]() +n(其中O为坐标原点),则函数y=f(x)的值域是( )
+n(其中O为坐标原点),则函数y=f(x)的值域是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.![]()
C.[﹣1,1]
D.(﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的AB,DC)和两个半圆构成,设AB=xm,且x≥80. 
(1)若内圈周长为400m,则x取何值时,矩形ABCD的面积最大?
(2)若景观带的内圈所围成区域的面积为 ![]() m2 , 则x取何值时,内圈周长最小?
m2 , 则x取何值时,内圈周长最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为π.
的最小正周期为π.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)若a,b,c分别为△ABC的三内角A,B,C的对边,角A是锐角,f(A)=0,a=1,b+c=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com