夹在直二面角α-MN-β两面间的一线段AB,与两面所成的角分别为30°和45°,过端点A、B分别作棱MN的垂线,垂足为C、D,若AB=5cm,求CD的长.
【答案】
分析:利用面面垂直的性质定理、线面角的定义及含30°、45°的直角三角形的边角关系、勾股定理即可得出.
解答:解:如图所示:

∵AC⊥MN,α⊥β,∴AC⊥β,∴AC⊥BC,
∴∠ABC是斜线AB与平面β所成的角,∴∠ABC=45°.
∵BD⊥MN,α⊥β,∴BD⊥α,∴BD⊥DA,
∴∠BAD是斜线AB与平面α所成的角,∴∠BAD=30°.
在Rt△ABD中,∵∠BAD=30°,AB=5,∴AD=ABcos30°=
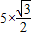
=
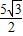
.
在Rt△ABC中,∵∠ABC=45°,AB=5,∴
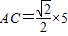
=

.
在Rt△ACD中,由勾股定理可得
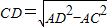
=
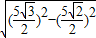
=

=2.5cm.
点评:熟练掌握面面垂直的性质定理、线面角的定义及含30°、45°的直角三角形的边角关系、勾股定理是解题的关键.


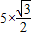 =
=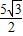 .
.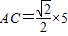 =
= .
.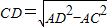 =
=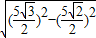 =
= =2.5cm.
=2.5cm.

 科学实验活动册系列答案
科学实验活动册系列答案