
【题目】已知集合A={x||2x﹣1|≤3},集合B={x|x2+(4﹣a)x﹣4a>0},若A∩B=A,求实数a的取值范围.
【答案】解:由题意:集合A={x||2x﹣1|≤3}={x|﹣1≤x≤2}
集合B={x|x2+(4﹣a)x﹣4a>0}={x|(x+4)(x﹣a)>0},
∵A∩B=A
∴AB.
解法一:
令f(x)=x2+(4﹣a)x﹣4a>0,
∵﹣1≤x≤2,
根据一元二次方程的根的分布:
可得: 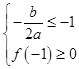 或
或 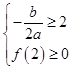
解:a≤﹣1
故得实数a的取值范围是:(﹣∞,﹣1].
解法二,讨论思想:
当a=﹣4时,B={x∈R|x≠﹣4},满足AB.
当a>﹣4时,B={x|x>a或x<﹣4},
要使AB成立,则:a≤﹣1.
当a<﹣4时,B={x|x<a或x>﹣4},满足AB.
故得实数a的取值范围是:(﹣∞,﹣1]
【解析】确定集合A的元素范围,根据A∩B=A,建立条件关系即可求实数a的取值范围.


科目:高中数学 来源: 题型:
【题目】下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数,满分为100),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为( ) 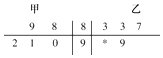
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=![]() (0<x≤120).已知甲、乙两地相距100千米.
(0<x≤120).已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2 , 四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm. 
(1)设矩形栏目宽度为xcm,求矩形广告面积S(x)的表达式
(2)怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥的侧棱![]() 底面
底面![]() ,且底面
,且底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在侧棱上.
在侧棱上.
(1)求证:![]() 平面
平面![]() ;
;
(2)若侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C:ρ=2acosθ(a>0),l:ρcos(θ﹣![]() )=
)=![]() , C与l有且仅有一个公共点.
, C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且∠AOB=![]() , 求|OA|+|OB|的最大值.
, 求|OA|+|OB|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com