
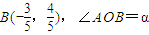 .
.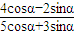 的值;
的值;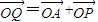 ,四边形OAQP的面积为S,
,四边形OAQP的面积为S,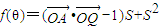 ,求f(θ)的最大值及此时θ的值.
,求f(θ)的最大值及此时θ的值.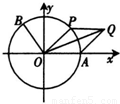
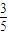 ,
,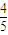 ),根据三角函数的定义,可求出α的正切值,进而利用弦化切技巧可求出
),根据三角函数的定义,可求出α的正切值,进而利用弦化切技巧可求出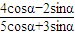 的值.
的值.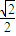 sin(2θ-
sin(2θ-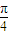 )+1,由此根据正弦函数的定义域和值域求得f(θ)的最大值及此时θ的值.
)+1,由此根据正弦函数的定义域和值域求得f(θ)的最大值及此时θ的值.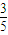 ,
,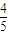 ),∴tanα=
),∴tanα=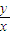 =
=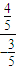 =-
=- .
.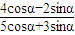 =
=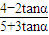 =
=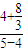 =
= .
.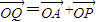 ,故四边形OAQP为平行四边形,
,故四边形OAQP为平行四边形, ×1×1sinθ=sinθ.
×1×1sinθ=sinθ.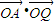 =
=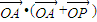 =
=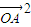 +
+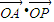 =1+cosθ.
=1+cosθ.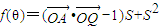 =cosθ•sinθ+sin2θ=
=cosθ•sinθ+sin2θ= sin2θ+
sin2θ+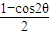 =
=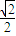 sin(2θ-
sin(2θ-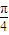 )+1,
)+1,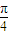 )=1,即 2θ-
)=1,即 2θ-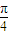 =
=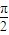 时,即 θ=
时,即 θ=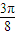 时,函数f(θ)取得最大值为
时,函数f(θ)取得最大值为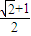 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
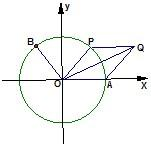 如图,A是单位圆与x轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),
如图,A是单位圆与x轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),| OQ |
| OA |
| OP |
| OA |
| OQ |
| 3 |
| 5 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
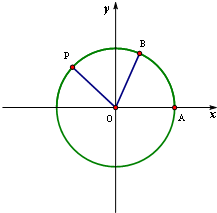 如图,A是单位圆与x轴正半轴的交点,B,P为单位圆上不同的点,∠AOB=θ,∠AOP=2θ,0≤θ≤π.
如图,A是单位圆与x轴正半轴的交点,B,P为单位圆上不同的点,∠AOB=θ,∠AOP=2θ,0≤θ≤π.| AB |
| OP |
| OQ |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
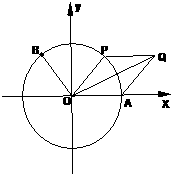 (2011•普宁市模拟)如图,A是单位圆与x轴正半轴的交点,点B、P在单位圆上,且B(-
(2011•普宁市模拟)如图,A是单位圆与x轴正半轴的交点,点B、P在单位圆上,且B(-| 3 |
| 5 |
| 4 |
| 5 |
| OQ |
| OA |
| OP |
| OA |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
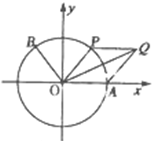 (2012•茂名二模)如图,A是单位圆与x轴正半轴的交点,点B,P在单位圆上,且B(-
(2012•茂名二模)如图,A是单位圆与x轴正半轴的交点,点B,P在单位圆上,且B(-| 3 |
| 5 |
| 4 |
| ,5 |
| OQ |
| OA |
| OP |
| π |
| 6 |
| OA |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•泸州一模)如图,A是单位圆与x轴正半轴的交点,点B、P在单位圆上,且B(-
(2012•泸州一模)如图,A是单位圆与x轴正半轴的交点,点B、P在单位圆上,且B(-| 3 |
| 5 |
| 4 |
| 5 |
| 4cosα-2sinα |
| 5cosα+3sinα |
| OQ |
| OA |
| OP |
| OA |
| OQ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com