
已知函数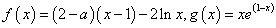 (
(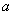 为常数,
为常数,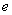 为自然对数的底)
为自然对数的底)
(1)当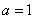 时,求
时,求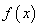 的单调区间;
的单调区间;
(2)若函数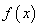 在
在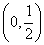 上无零点,求
上无零点,求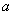 的最小值;
的最小值;
(3)若对任意的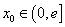 ,在
,在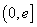 上存在两个不同的
上存在两个不同的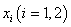 使得
使得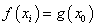 成立,求
成立,求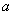 的取值范围.
的取值范围.
(1)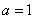 时,
时,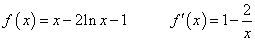
由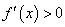 得
得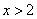
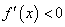 得
得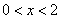
故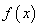 的减区间为
的减区间为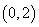 增区间为
增区间为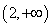
(2)因为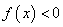 在
在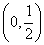 上恒成立不可能
上恒成立不可能
故要使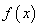 在
在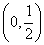 上无零点,只要对任意的
上无零点,只要对任意的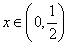 ,
,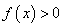 恒成立
恒成立
即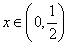 时,
时,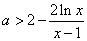
令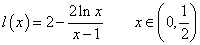
则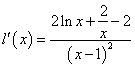
再令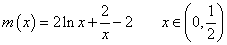
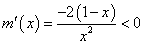 于是在
于是在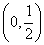 上
上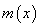 为减函数
为减函数
故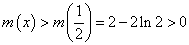
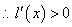 在
在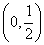 上恒成立
上恒成立
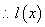 在
在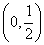 上为增函数
上为增函数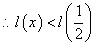 在
在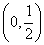 上恒成立
上恒成立
又 故要使
故要使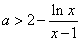 恒成立,只要
恒成立,只要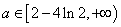
若函数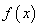 在
在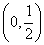 上无零点,
上无零点,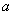 的最小值为
的最小值为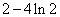
(3)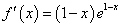
当 时,
时,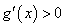 ,
,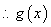 为增函数
为增函数
当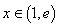 时,
时,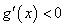 ,
,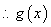 为减函数
为减函数
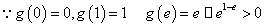
 函数
函数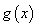 在
在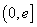 上的值域为
上的值域为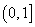
 当
当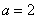 时,不合题意
时,不合题意
当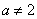 时,
时,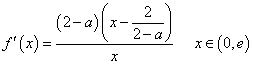
故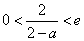
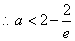 ①
①
此时,当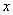 变化时,
变化时,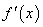 ,
,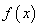 的变化情况如下
的变化情况如下
|
|
|
|
|
|
| — | 0 | + |
|
| ↘ | 最小值 | ↗ |
 时,
时,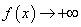 ,
,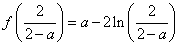
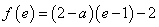
 任意定的
任意定的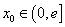 ,在区间
,在区间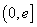 上存在两个不同的
上存在两个不同的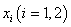
使得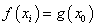 成立,
成立,
当且仅当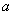 满足下列条件
满足下列条件
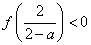 即
即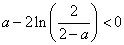 ②
②
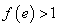 即
即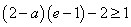 ③
③
令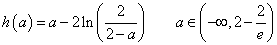
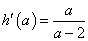 令
令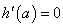 得
得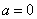
当 时,
时,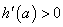 函数
函数 为增函数
为增函数
当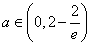 时,
时,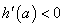 函数
函数 为减函数
为减函数
所以在任取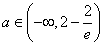 时有
时有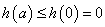 即②式对
即②式对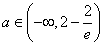 恒成立
恒成立
由③解得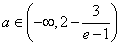 ④
④
由①④ 当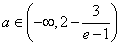 时
时
对任意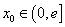 ,在
,在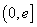 上存在两个不同的
上存在两个不同的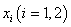 使
使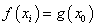 成立
成立


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
用某种方法来选择不超过100的正整数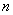 ,若
,若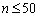 ,那么选择
,那么选择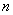 的概率是
的概率是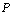 ;若
;若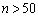 ,那么选择
,那么选择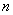 的概率是
的概率是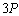 ,则选择到一个完全平方数
,则选择到一个完全平方数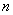 的概率是 ( )
的概率是 ( )
A.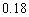 B.
B.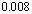 C.
C.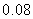 D.0.8
D.0.8
查看答案和解析>>
科目:高中数学 来源: 题型:
经过两点(-1,8)和(4,-2)的直线的两点式方程是____________________,截距式方程是__________________,一般式方程是____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com