
若点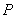 在曲线
在曲线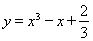 上移动,设点
上移动,设点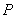 处的切线的倾斜角为
处的切线的倾斜角为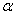 ,则
,则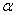 的范围是______.
的范围是______.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| p |
| |OM| |
| |MN| |
| 1 |
| |NA| |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年海南省海口市高考调研考试数学(理) 题型:解答题
(本小题满分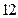 分)在平面直角坐标系中,已知两个定点
分)在平面直角坐标系中,已知两个定点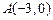 和
和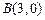 .动点
.动点 在
在 轴上的射影是
轴上的射影是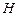 (
(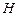 随
随 移动而移动),若对于每个动点M总存在相应的点
移动而移动),若对于每个动点M总存在相应的点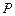 满足
满足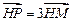 ,且
,且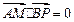 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过定点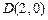 的直线
的直线 (直线
(直线 与
与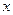 轴不重合)交曲线
轴不重合)交曲线 于
于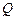 ,
,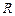 两点,求证:直线
两点,求证:直线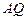 与直线
与直线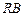 交点总在某直线
交点总在某直线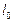 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,△ABC为直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 轴上,且AM=
轴上,且AM=![]() ,点C在
,点C在![]() 轴上移动.
轴上移动.
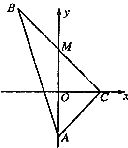
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,![]() )的直线
)的直线![]() 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,![]() )(
)(![]() <0),
<0),![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ≤
≤![]() 等恒成立,求
等恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以![]() 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
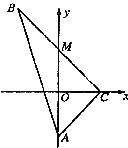 如图所示,△ABC为直角三角形,∠C=90°,若
如图所示,△ABC为直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 轴上,且AM=
轴上,且AM=![]() ,点C在
,点C在![]() 轴上移动.
轴上移动.
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,![]() )的直线
)的直线![]() 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,![]() )(
)(![]() <0),
<0),![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ≤
≤![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以![]() 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
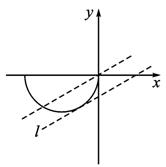
(1)试问点P的轨迹是什么曲线?
(2)已知直线l的斜率为![]() ,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com