
 下,目标函数z=2x+3y的最小值为 ,最大值为 .
下,目标函数z=2x+3y的最小值为 ,最大值为 . 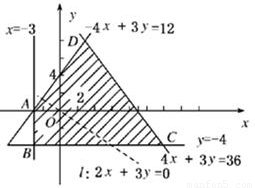 解:作出可行域(如图阴影部分).
解:作出可行域(如图阴影部分).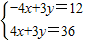 ,可以求得顶点D的坐标为(3,8).
,可以求得顶点D的坐标为(3,8).

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:2014届福建省高一下学期期末数学试卷(解析版) 题型:填空题
若在约束条件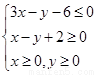 下
,目标函数
下
,目标函数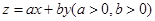 的最大值为12.给出下列四个判断:
的最大值为12.给出下列四个判断:
①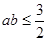 ; ②
; ②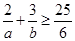 ; ③
; ③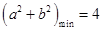 ; ④
; ④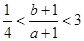 .
.
其中正确的判断是 .(请写出所有正确判断的序号)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市鄞州区高三5月高考适应性文科数学试卷(解析版) 题型:填空题
设m>1,在约束条件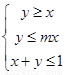 下,目标函数z=x+my的最大值小于2,则m的取值
下,目标函数z=x+my的最大值小于2,则m的取值
范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com