【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准，新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升，小于80毫克/百毫克升为饮酒驾车，血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车，经过反复试验，喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下：
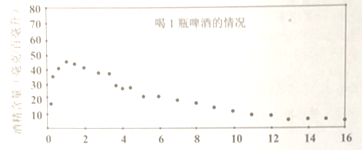
该函数模型如下：
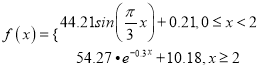
根据上述条件，回答以下问题：
（1）试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值？最大值是多少？
（2）试计算喝1瓶啤酒后多少小时后才可以驾车？（时间以整小时计算）
（参数数据： 
， 
， 
）
【答案】（1）喝1瓶啤酒后1.5小时血液中的酒精含量达到最大值44.42毫克/百毫升；（2）喝1瓶啤酒后需6小时后才可以合法驾车.
【解析】试题分析：（1）由图可知，当函数
取得最大值时， 
，根据函数模型，即可求出最大值；（2））由题意知，当车辆驾驶人员血液中的酒精小于20毫克/百毫升时可以驾车，此时
，然后解不等式
，即可求出.
试题解析：（1）由图可知，当函数
取得最大值时， 
，
此时
，
当
，即
时，函数
取得最大值为
.
故喝1瓶啤酒后1.5小时血液中的酒精含量达到最大值44.42毫克/百毫升.
（2）由题意知，当车辆驾驶人员血液中的酒精小于20毫克/百毫升时可以驾车，此时
.
由
，得： 
，
两边取自然对数得： 
即
，
∴
，故喝1瓶啤酒后需6小时后才可以合法驾车.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图，平面五边形ABCDE中，AB∥CE，且AE＝2，∠AEC＝60°，CD＝ED＝
，cos∠EDC＝
.将△CDE沿CE折起，使点D移动到P的位置，且AP＝
，得到四棱锥P－ABCE.
(1)求证：AP⊥平面ABCE；
(2)记平面PAB与平面PCE相交于直线l，求证：AB∥l.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a、b、c为△ABC的三个内角A、B、C的对边，向量
=（-1，
），
=（cosA，sinA），若⊥，且acosB+bcosA=csinC，则角B的大小为______．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种植基地将编号分别为1，2，3，4，5，6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验，要求这六块实验田分别种植不同品种的马铃薯，若种植时要求编号1，3，5的三个品种的马铃薯中至少有两个相邻，且2号品种的马铃薯不能种植在A、F这两块实验田上，则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在原点的椭圆
的两焦点分别为双曲线
的顶点，直线
与椭圆交于
、
两点，且
，点
是椭圆上异于、的任意一点，直线
外的点
满足
， 
．
（1）求点的轨迹方程；
（2）试确定点的坐标，使得
的面积最大，并求出最大面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着电商的快速发展，快递业突飞猛进，到目前，中国拥有世界上最大的快递市场.某快递公司收取快递费的标准是：重量不超过
的包裹收费10元；重量超过的包裹，在收费10元的基础上，每超过（不足，按计算）需再收5元.
该公司将最近承揽的100件包裹的重量统计如下：
公司对近60天，每天揽件数量统计如下表：
以上数据已做近似处理，并将频率视为概率.
（1）计算该公司未来5天内恰有2天揽件数在101~300之间的概率；
（2）①估计该公司对每件包裹收取的快递费的平均值；
②根据以往的经验，公司将快递费的三分之一作为前台工作人员的工资和公司利润，其余的用作其他费用.目前前台有工作人员3人，每人每天揽件不超过150件，日工资100元.公司正在考虑是否将前台工作人员裁减1人，试计算裁员前后公司每日利润的数学期望，若你是决策者，是否裁减工作人员1人？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面直角坐标系
，以
为极点，
轴的非负半轴为极轴建立极坐标系，
点的极坐标为
，直线
的极坐标方程为
，曲线
的参数方程为
（
为参数）.
（1）写出点的直角坐标及曲线的直角坐标方程；
（2）若
为曲线上的动点，求
中点
到直线的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
