Question

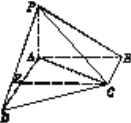
【题目】如图，平面五边形ABCDE中，AB∥CE，且AE＝2，∠AEC＝60°，CD＝ED＝，cos∠EDC＝.将△CDE沿CE折起，使点D移动到P的位置，且AP＝，得到四棱锥P－ABCE.

(1)求证：AP⊥平面ABCE；

(2)记平面PAB与平面PCE相交于直线l，求证：AB∥l.

Answer 1

【答案】(1)证明见解析；(2)证明见解析.

【解析】试题分析：

（1）在中，由已知结合余弦定理得，连接，可得，在中，由，得，同理，然后利用线面垂直的判定可得平面；

（2）由，且平面， 平面，可得平面，又平面平面，结合面面平行的性质可得.

试题解析：

(1)在△CDE中，

∵CD＝ED＝，cos∠EDC＝，

由余弦定理，CE2＝()2＋()2－2×××＝4，

∴CE＝2.连接AC，

∵AE＝2，∠AEC＝60°，∴AC＝2.

又∵AP＝，

∴在△PAE中，PA2＋AE2＝PE2，即AP⊥AE，同理AP⊥AC，而AC，AE平面ABCE，AC∩AE＝A，

故AP⊥平面ABCE.

(2)∵AB∥CE，且CE平面PCE，AB平面PCE，

∴AB∥平面PCE.

又平面PAB∩平面PCE＝l，∴AB∥l.