
【题目】已知椭圆E: ![]() ,其焦点为F1,F2,离心率为
,其焦点为F1,F2,离心率为![]() ,直线l:x+2y-2=0与x轴,y轴分别交于点A,B,
,直线l:x+2y-2=0与x轴,y轴分别交于点A,B,
(1)若点A是椭圆E的一个顶点,求椭圆的方程;
(2)若线段AB上存在点P满足|PF1|+|PF2|=2a,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)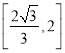
【解析】试题分析:(1)先利用直线方程求出椭圆的右顶点,再由离心率进行求解;(2)将问题转化为判定直线和椭圆有公共点,联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用判别式进行求解.
的一元二次方程,利用判别式进行求解.
试题解析:(1)由椭圆的离心率为![]() ,
,
得a=![]() c,∵直线l与x轴交于A点,
c,∵直线l与x轴交于A点,
∴A(2,0),∴a=2,c=![]() ,b=
,b=![]() ,
,
∴椭圆方程为![]() +
+![]() =1.
=1.
(2)由e=![]() ,可设椭圆E的方程为
,可设椭圆E的方程为![]() +
+![]() =1,
=1,
联立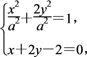
得6y2-8y+4-a2=0,
若线段AB上存在点P满足|PF1|+|PF2|=2a,则线段AB与椭圆E有公共点,等价于方程6y2-8y+4-a2=0在y∈[0,1]上有解.
设f(y)=6y2-8y+4-a2,
∴![]() 即
即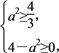
∴![]() ≤a2≤4,
≤a2≤4,
故a的取值范围是![]() ≤a≤2.
≤a≤2.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系和直角坐标系中,极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合,曲线
轴的非负半轴重合,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)判断曲线![]() 与曲线
与曲线![]() 的位置关系,若两曲线相交,求出两交点间的距离.
的位置关系,若两曲线相交,求出两交点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,将木兰溪流经市区河段分成![]() 段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)记评分在![]() 以上(包括
以上(包括![]() )为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(Ⅱ)根据表中数据完成下面茎叶图;
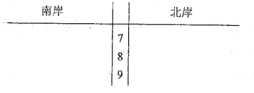
(Ⅲ)分别估计两岸分值的中位数,并计算它们的平均值,试从计算结果分析两岸环保情况,哪边保护更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() 的离心率为
的离心率为![]() ,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆G相交于B,C两点,请判断直线MB,MC是否关于直线m对称,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sinωxcosωx-cos2ωx+
sinωxcosωx-cos2ωx+![]() (ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
(ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | -1 | 0 |
(1)请直接写出①处应填的值,并求函数f(x)在区间![]() 上的值域;
上的值域;
(2)△ABC的内角A,B,C所对的边分别为a,b,c,已知f(A+![]() )=1,b+c=4,a=
)=1,b+c=4,a=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数图象的对称性与周期性,有下列说法:①若函数y=f(x)满足f(x+1)=f(3+x),则f(x)的一个周期为T=2;②若函数y=f(x)满足f(x+1)=f(3-x),则f(x)的图象关于直线x=2对称;③函数y=f(x+1)与函数y=f(3-x)的图象关于直线x=2对称;④若函数![]() 与函数f(x)的图象关于原点对称,则
与函数f(x)的图象关于原点对称,则![]() ,其中正确的个数是()
,其中正确的个数是()
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=![]() ,cos∠EDC=
,cos∠EDC=![]() .将△CDE沿CE折起,使点D移动到P的位置,且AP=
.将△CDE沿CE折起,使点D移动到P的位置,且AP=![]() ,得到四棱锥P-ABCE.
,得到四棱锥P-ABCE.
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com