【题目】已知数列的前项和为，且对任意正整数，都有成立．记．

（Ⅰ）求数列和的通项公式；

（Ⅱ）设，数列的前项和为，求证： ．

参考答案：

【答案】（Ⅰ）, （Ⅱ）见解析.

【解析】试题分析：（I）由成立，可得时， ，可得出数列为等比数列,从而可得数列的通项公式，根据对数的运算性质可得；(II)利用（I）的结论，可得，根据裂项求和求出数列的前项和为,再利用放缩法即可证明结论.

试题解析：（Ⅰ）在中，令得.

因为对任意正整数，都有成立， 时， ，

两式作差得， ，所以，

又，所以数列是以为首项，4为公比的等比数列，即，

∴

（Ⅱ）∵，

∴.

∴.

∴对任意， ．

又，所以， 为关于的增函数，所以，

综上，

【方法点晴】本题主要考查等差数列的通项与等比数列的定义，以及裂项相消法求数列的和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1) ；（2） ； （3）；（4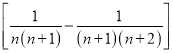） ；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.

关闭