【答案】
分析:先记有0和1的为A卡,写有6和7的为B卡,另两张为C卡;
(1)根据题意,分有无A卡2种情况讨论,由分步计数原理计算每种情况下的三位数的个数,再由分类计数原理将两种情况下的三位数的个数相加,即可得答案;
(2)由数列的性质分析可得B卡正反两面有3种用法,其余的卡都有2种用法,分有无B卡2种情况讨论,由分步计数原理计算可得数列的个数,将其相加可得全部数列的情况数目,列举可得三个数依次等差数列的情况数目,由等可能事件的概率公式,计算可得答案.
解答:解:记写有0和1的为A卡,写有6和7的为B卡,另两张为C卡;
(1)根据题意,三位数的首位不能为0,分2种情况讨论:
①无A卡时,一张B卡和两张C卡可以作任意的排列,并且每一张卡的正反两面都可用,其中B卡的两个面有3种用法,故可组成
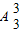
×3×2×2=72个三位数;
②有A卡时,再分有无B卡讨论:
(Ⅰ)有B卡的,A卡在百位时:有C
21A
22×3×2=24个,A卡不在百位时,有C
21C
21A
22×3×2×2=96个,
(Ⅱ)无B卡的,A卡在百位时:有A
22×2×2=8个,A卡不在百位时,有C
21A
22×2×2×2=32个,
故共有N=72+24+96+8+32=232个三位整数.
(2)数列的首项可以为0,
故A卡、B卡、C卡都不受排列位置的限制,但B卡正反两面有3种用法,其余的卡都有2种用法.
任选3张卡排成一列,有B卡时可得C
32×A
33×3×2×2=216个,
无B卡时有A
33×2×2×2=48个,共有216+48=264个,
其中三个数依次等差数列的情况有0,2,4和4,2,0;0,3,6和6,3,0;1,3,5和5,3,1;1,4,7和7,4,1;2,4,6和6,4,2;3,5,7和7,5,3;1,5,9和9,5,1;共14个;
故所求的概率为P=
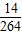
=
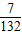
.
点评:本题考查排列、组合的应用,分步、分类计数原理的应用以及等可能事件的概率计算;对于(1)、(2)要注意三位数与排列的区别.

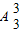 ×3×2×2=72个三位数;
×3×2×2=72个三位数; 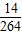 =
=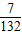 .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案