
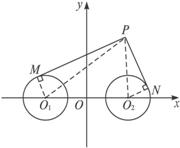
思路点拨:本题是解析几何中求轨迹方程问题,按求轨迹方程问题的一般方法步骤求解即可.
解:如图,以直线O1O2为x轴,线段O1O2的垂直平分线为y轴,建立平面直角坐标系,则两圆心的坐标分别为O1(-2,0),O2(2,0).

设P(x,y),则PM2=PO12-MO12=(x+2)2+y2-1.
同理,PN2=(x-2)2+y2-1.
PM=![]() PN,即(x+2)2+y2-1=2[(x-2)2+y2-1],
PN,即(x+2)2+y2-1=2[(x-2)2+y2-1],
即x2-12x+y2+3=0,
即(x-6)2+y2=33.这就是动点P的轨迹方程.
[一通百通]本题是考查解析几何中求点的轨迹方程的方法应用,考查建立坐标系、数形结合思想、勾股定理、两点间距离公式等知识内容,及分析推理、计算化简技能、技巧等,是一道很综合的题目.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
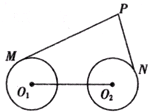 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得PM=
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得PM=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
|
|
| α |
| α |
| β |
|
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
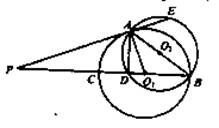
如图,圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点.
求证:(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com