
已知各项均不为零的数列{an}的前n项和为Sn,且满足a1=c,2Sn=anan+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求![]() 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由.
(2)设![]() ,
,![]() ,
,
若r>c>4,求证:对于一切n∈N*,不等式![]() 恒成立.
恒成立.
解:(1)n=1时,2a1=a1a2+r,∵a1=c≠0,∴2c=ca2+r,![]() . (1分)
. (1分)
n≥2时,2Sn=anan+1+r,① 2Sn-1=an-1an+r,②
①-②,得2an=an(an+1-an-1).∵an≠0,∴an+1-an-1=2. ( 3分)
则a1,a3,a5,…,a2n-1,… 成公差为2的等差数列,a2n-1=a1+2(n-1).
a2,a4,a6,…,a2n,… 成公差为2的等差数列, a2n=a2+2(n-1).
要使{an}为等差数列,当且仅当a2-a1=1.即![]() .r=c-c2. ( 4分)
.r=c-c2. ( 4分)
∵r=-6,∴c2-c-6=0,c=-2或3.
∵当c=-2,![]() ,不合题意,舍去.
,不合题意,舍去.
∴当且仅当![]() 时,数列
时,数列![]() 为等差数列 (5分)
为等差数列 (5分)
(2)![]() =[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=
=[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=![]() -2.
-2.
![]() =[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(
=[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(![]() ). (8分)
). (8分)
∴![]()
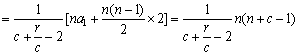 (9分)
(9分)
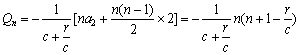 . (10分)
. (10分)
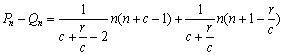 =
=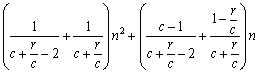 .(11分)
.(11分)
∵r>c>4,∴![]() >4,∴
>4,∴![]() >2.∴0<
>2.∴0<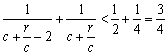 <1. (13分)
<1. (13分)
且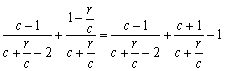 >-1. (14分)
>-1. (14分)
又∵r>c>4,∴![]() ,则0<
,则0<![]() .
.![]() .
.
∴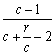 <1.
<1.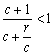 .∴
.∴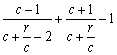 <1.(15分)
<1.(15分)
∴对于一切n∈N*,不等式![]() 恒成立.(16分)
恒成立.(16分)
附加题部分


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| a6 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| cn |
| bn |
A、若?n∈N*总有
| ||||
B、若?n∈N*总有
| ||||
C、若?n∈N*总有
| ||||
D、若?n∈N*总有
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| an |
| 2 |
| k-1 |
| 3n+4 |
| 3n+5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a1 |
| a1-a2 |
| a1 |
| a1-a2 |
| a3 |
| a3-a4 |
| a2n-1 |
| a2n-1-a2n |
| a2 |
| a2-a3 |
| a4 |
| a4-a5 |
| a2n |
| a2n-a2n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com