
分析 先求二次函数图象的对称轴,因为开口向下,因此求最大值,根据对称轴分三种情况讨论,分别求出最大值和最小值.
解答 解:y=f(x)=-x2+2ax=-(x-a)2+a2,
函数y=-x2-2ax+1的图象是开口朝下,且以直线x=a为对称轴的抛物线,
当0<a≤$\frac{1}{2}$时,函数在[0,a]上为增函数,在(a,1)上为减函数,x=a时,函数最大值为:a2,当x=1时,函数最小值为:2a-1;
当$\frac{1}{2}$<a<1时,函数在[0,a]上为增函数,在(a,1)上为减函数,x=a时,函数最大值为:a2,当x=0时,函数最小值为:0;
当a>1时,函数在[0,1]上为增函数,x=1时,函数最大值为:1,当x=0时,函数最小值为:0.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
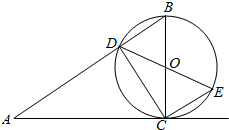 如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.
如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com