
【题目】设函数![]()
(Ⅰ)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的极小值;
的极小值;
(Ⅱ)若函数![]() 存在唯一零点,求
存在唯一零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 的极小值为2;(Ⅱ)当
的极小值为2;(Ⅱ)当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.
【解析】试题分析:(1)先求导数,再求导函数零点,列表分析导函数符号变化规律,进而确定极值(2)先化简![]() ,再利用参变分离法得
,再利用参变分离法得![]() ,利用导数研究函数
,利用导数研究函数![]() ,由图像可得存在唯一零点时
,由图像可得存在唯一零点时![]() 的取值范围
的取值范围
试题解析:(1)由题设,当![]() 时,
时, ![]() ,
,
则![]() ,由
,由![]() ,得
,得![]() .
.
∴当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时, ![]() 取得极小值
取得极小值![]() ,
,
∴![]() 的极小值为2.
的极小值为2.
(2)由题设![]() ,
,
令![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() 是
是![]() 的唯一极值点,且是极大值点,因此
的唯一极值点,且是极大值点,因此![]() 也是
也是![]() 的最大值点.
的最大值点.
∴![]() 的最大值为
的最大值为![]() .
.
又![]() ,结合
,结合![]() 的图象(如图),可知
的图象(如图),可知
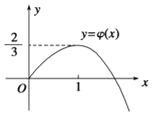
当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
当![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.
所以,当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.


科目:高中数学 来源: 题型:
【题目】平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1 , α∩平面ABCD=m,α∩平面ABB1A1=n,则m、n所成角的正弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知长方形ABCD中,AB=2,AD=1,E为DC的中点.将△ADE沿AE折起,使得平面ADE⊥平面ABCE. 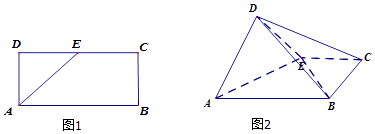
(1)求证:平面BDE⊥平面ADE
(2)求三棱锥 C﹣BDE的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求实数a的值,并判断f(x)的单调性(不用证明);
(2)已知不等式f(logm ![]() )+f(﹣1)>0恒成立,求实数m的取值范围.
)+f(﹣1)>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在平行四边形ABB1A1中,∠ABB1=60°,AB=4,AA1=2,C,C1分别为AB,A1B1的中点,现把平行四边形ABB1A1沿CC1折起如图2所示,连接B1C,B1A,B1A1 . 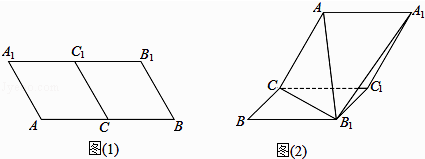
(1)求证:AB1⊥CC1;
(2)若AB1= ![]() ,求二面角C﹣AB1﹣A1的余弦值.
,求二面角C﹣AB1﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则sinAcosBsinC=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数 ![]() ,看下面四个结论( )
,看下面四个结论( )
①f(x)是奇函数;②当x>2007时, ![]() 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ![]() ;④f(x)的最小值是
;④f(x)的最小值是 ![]() .其中正确结论的个数为:
.其中正确结论的个数为:
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 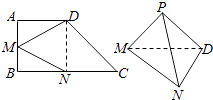
(1)证明:平面PMD⊥平面PND;
(2)若cos∠DNP= ![]() ,PD=5,求直线PD与平面DMN所成角的正弦值.
,PD=5,求直线PD与平面DMN所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com