练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设M是满足下列两个条件的函数f(x)的集合：

    ①f(x)的定义域是[－1，1]；

    ②若x1，x2∈[－1，1]，则|f(x1)－f(x2)|≤4|x1－x2|．

    试问：定义在[－1，1]上的函数g(x)＝x2＋2x－1是否属于集合M？并说明理由．

    答案：
    解析：

    		 　　思路　　只要对g(x)判定②中绝对值不等式是否成立

    　　思路　　只要对g(x)判定②中绝对值不等式是否成立．

    　　解答　　显然g(x)满足条件①．

    　　设x1，x2∈[－1，1]，则|x1|≤1，|x2|≤1．

    　　∵|g(x1)－g(x2)}

    　　＝|(＋2x1－1)－(＋2x2－1)|

    　　＝|(x1－x2)(x1＋x2＋2)|

    　　＝|x1－x2|·|x1＋x2＋2|

    　　≤(|x1|＋|x2|＋2)·|x1－x2|

    　　≤4|x1－x2|．

    　　∴函数g(x)满足条件②．

    　　故g(x)∈M．

    　　评析　　要说明函数g(x)∈M，必须证明g(x)同时满足条件①和②．本题关键是要读懂题意，熟悉绝对值不等式的性质．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2010•朝阳区二模）设A是满足下列两个条件的无穷数列{an}的集合：
    ①
    an+an+22
    ≤an+1    ；     ②an≤M．其中n∈N*，M是与n无关的常数．
    （Ⅰ）若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，证明：{Sn}∈A；
    （Ⅱ）对于（Ⅰ）中数列{an}，正整数n1，n2，…，nt…（t∈N*）满足7＜n1＜n2＜…＜nt＜…（t∈N*），并且使得a6，a7，an1，an2，…，ant，…成等比数列． 若bm=10m-nm（m∈N*），则{bm}∈A是否成立？若成立，求M的取值范围，若不成立，请说明理由；
    （Ⅲ）设数列{cn}的各项均为正整数，且{cn}∈A，证明：cn≤cn+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设A是满足下列两个条件的无穷数列{an}的集合：
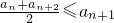    ①数学公式；　　 ②an≤M．其中n∈N*，M是与n无关的常数．
    （Ⅰ）若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，证明：{Sn}∈A；
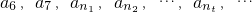    （Ⅱ）对于（Ⅰ）中数列{an}，正整数n1，n2，…，nt…（t∈N*）满足7＜n1＜n2＜…＜nt＜…（t∈N*），并且使得数学公式成等比数列． 若bm=10m-nm（m∈N*），则{bm}∈A是否成立？若成立，求M的取值范围，若不成立，请说明理由；
    （Ⅲ）设数列{cn}的各项均为正整数，且{cn}∈A，证明：cn≤cn+1．

    查看答案和解析>>

    科目：高中数学 来源：朝阳区二模 题型：解答题

    设A是满足下列两个条件的无穷数列{an}的集合：
    ①
    an+an+2
    2
    ≤an+1    ；     ②an≤M．其中n∈N*，M是与n无关的常数．
    （Ⅰ）若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，证明：{Sn}∈A；
    （Ⅱ）对于（Ⅰ）中数列{an}，正整数n1，n2，…，nt…（t∈N*）满足7＜n1＜n2＜…＜nt＜…（t∈N*），并且使得a6，a7，an1，an2，…，ant，…成等比数列． 若bm=10m-nm（m∈N*），则{bm}∈A是否成立？若成立，求M的取值范围，若不成立，请说明理由；
    （Ⅲ）设数列{cn}的各项均为正整数，且{cn}∈A，证明：cn≤cn+1．

    查看答案和解析>>

    科目：高中数学 来源：2010年北京市朝阳区高考数学三模试卷（理科）（解析版） 题型：解答题

    设A是满足下列两个条件的无穷数列{an}的集合：
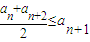    ①；     ②an≤M．其中n∈N*，M是与n无关的常数．
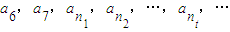    （Ⅰ）若{an}是等差数列，Sn是其前n项的和，a3=4，S3=18，证明：{Sn}∈A；
    （Ⅱ）对于（Ⅰ）中数列{an}，正整数n1，n2，…，nt…（t∈N*）满足7＜n1＜n2＜…＜nt＜…（t∈N*），并且使得成等比数列． 若bm=10m-nm（m∈N*），则{bm}∈A是否成立？若成立，求M的取值范围，若不成立，请说明理由；
    （Ⅲ）设数列{cn}的各项均为正整数，且{cn}∈A，证明：cn≤cn+1．

    查看答案和解析>>

    同步练习册答案