
分析 (Ⅰ)将$\overrightarrow{OC}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$代入$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$,然后进行向量的数乘运算即可得出$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AB}$,从而得出A,B,C三点共线;
(Ⅱ)由条件即可求出$\overrightarrow{OC},\overrightarrow{AB}$的坐标,进而求出$\overrightarrow{OA}•\overrightarrow{OC}$,及$|\overrightarrow{AB}|$的值,代入$f(x)=\overrightarrow{OA}•\overrightarrow{OC}-(2{m}^{2}+\frac{2}{3})|\overrightarrow{AB}|$并化简即可得出f(x)=-sin2x-2m2sinx+2,而配方即可得出sinx=1时,f(x)取最小值$\frac{1}{2}$,从而得到$-(1+{m}^{2})^{2}+{m}^{4}+2=\frac{1}{2}$,这样即可解出m的值.
解答 解:(Ⅰ)证明:根据条件:
$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$
=$\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\overrightarrow{OA}$
=$\frac{2}{3}(\overrightarrow{OB}-\overrightarrow{OA})$
=$\frac{2}{3}\overrightarrow{AB}$;
∴$\overrightarrow{AC}∥\overrightarrow{AB}$;
∴A,B,C三点共线;
(Ⅱ)根据条件:$\overrightarrow{OA}=(1,cosx),\overrightarrow{OB}=(1+sinx,cosx)$,$\overrightarrow{OC}=\frac{1}{3}(1,cosx)+\frac{2}{3}(1+sinx,cosx)$=$(1+\frac{2}{3}sinx,cosx)$,$\overrightarrow{AB}=(sinx,0)$,且$x∈[0,\frac{π}{2}]$;
∴$\overrightarrow{OA}•\overrightarrow{OC}=1+\frac{2}{3}sinx+co{s}^{2}x$=$-si{n}^{2}x+\frac{2}{3}sinx+2$,$|\overrightarrow{AB}|=sinx$;
∴$f(x)=-si{n}^{2}x+\frac{2}{3}sinx+2-(2{m}^{2}+\frac{2}{3})sinx$
=-sin2x-2m2sinx+2
=-(sinx+m2)2+m4+2;
又sinx∈[0,1];
∴sinx=1时,f(x)取最小值$\frac{1}{2}$;
即$-(1+{m}^{2})^{2}+{m}^{4}+2=\frac{1}{2}$;
∴${m}^{2}=\frac{1}{4}$;
∴$m=±\frac{1}{2}$.
点评 考查向量减法的几何意义,向量的数乘运算,共线向量基本定理,根据点的坐标求向量的坐标,以及向量数量积的坐标运算,配方法的运用.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
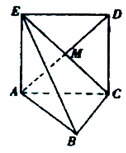 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com