
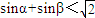 ;
;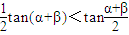 .
. 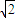 sin(α+45°)≤
sin(α+45°)≤ ,
, 成立;故②对.
成立;故②对.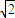 sin(α+45°)
sin(α+45°)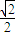 ⇒cosα+cosβ>
⇒cosα+cosβ> sin(α+45°)>1,故③对.
sin(α+45°)>1,故③对. ×tan(α+β)=
×tan(α+β)= ×tan60°=
×tan60°= ×
× =
=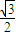 ;而tan
;而tan =tan30°=
=tan30°= 比
比 小,故等式不成立.即④不成立.
小,故等式不成立.即④不成立.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
| 2 |
| 1 |
| 2 |
| α+β |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、tanαtanβ<1 | ||||
B、sinα+sinβ<
| ||||
C、
| ||||
| D、cosα+cosβ>1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三下学期第二次联考理数学试卷 题型:选择题
已知 外接圆
外接圆 的半径为
的半径为 ,且
,且 .
. ,从圆
,从圆 内随机取一个点
内随机取一个点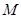 ,若点
,若点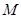 取自内的概率恰为
取自内的概率恰为 ,判断
,判断 的形状.( )
的形状.( )
A.直角三角形 B.等边三角形 C.钝角三角形 D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com