
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上. (Ⅰ)求异面直线D1E与A1D所成的角;
(Ⅱ)若二面角D1﹣EC﹣D的大小为45°,求点B到平面D1EC的距离.
【答案】解:解法一:(Ⅰ)连结AD1 . 由AA1D1D是正方形知AD1⊥A1D. ∵AB⊥平面AA1D1D,
∴AD1是D1E在平面AA1D1D内的射影.
根据三垂线定理得AD1⊥D1E,
则异面直线D1E与A1D所成的角为90°.
(Ⅱ)作DF⊥CE,垂足为F,连结D1F,则CE⊥D1F.
所以∠DFD1为二面角D1﹣EC﹣D的平面角,∠DFD1=45°.于是 ![]() ,
,
易得 Rt△BCE≌Rt△CDF,所以CE=CD=2,又BC=1,所以 ![]() .
.
设点B到平面D1EC的距离为h,则由于 ![]() ,即f'(x),
,即f'(x),
因此有CED1Fh=BEBCDD1 , 即 ![]() ,∴
,∴ ![]() .
.
解法二:如图,分别以DA,DC,DD1为x轴,y轴,z轴,建立空间直角坐标系.
(Ⅰ)由A1(1,0,1),得 ![]() ,
,
设E(1,a,0),又D1(0,0,1),则 ![]() .
.
∵ ![]() ∴
∴ ![]() ,则异面直线D1E与A1D所成的角为90°.
,则异面直线D1E与A1D所成的角为90°.
(Ⅱ) ![]() =(0,0,1)为面DEC的法向量,设
=(0,0,1)为面DEC的法向量,设 ![]() =(x,y,z)为面CED1的法向量,
=(x,y,z)为面CED1的法向量,
则 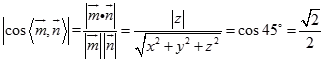 ,
,
∴z2=x2+y2 . ①
由C(0,2,0),得 ![]() ,则
,则 ![]() ,即
,即 ![]() ,∴2y﹣z=0②
,∴2y﹣z=0②
由①、②,可取 ![]() ,又
,又 ![]() ,
,
所以点B到平面D1EC的距离 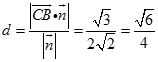
【解析】解法一:(Ⅰ)连结AD1 . 判断AD1是D1E在平面AA1D1D内的射影.得到异面直线D1E与A1D所成的角.(Ⅱ)作DF⊥CE,垂足为F,连结D1F,说明∠DFD1为二面角D1﹣EC﹣D的平面角,∠DFD1=45°.利用等体积法,求点B到平面D1EC的距离.解法二:分别以DA,DC,DD1为x轴,y轴,z轴,建立空间直角坐标系.(Ⅰ)通过向量的数量积为0,即可求异面直线D1E与A1D所成的角;(Ⅱ) ![]() =(0,0,1)为面DEC的法向量,设
=(0,0,1)为面DEC的法向量,设 ![]() =(x,y,z)为面CED1的法向量,通过二面角D1﹣EC﹣D的大小为45°,求出x、y、z的关系,结合
=(x,y,z)为面CED1的法向量,通过二面角D1﹣EC﹣D的大小为45°,求出x、y、z的关系,结合 ![]() ,求出平面的法向量,利用
,求出平面的法向量,利用 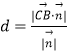 求点B到平面D1EC的距离.
求点B到平面D1EC的距离.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


科目:高中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 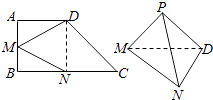
(1)证明:平面PMD⊥平面PND;
(2)若cos∠DNP= ![]() ,PD=5,求直线PD与平面DMN所成角的正弦值.
,PD=5,求直线PD与平面DMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点O是平行四边形ABCD两条对角线的交点,给出下列向量组:
① ![]() 与
与 ![]() ;
;
② ![]() 与
与 ![]() ;
;
③ ![]() 与
与 ![]() ;
;
④ ![]() 与
与 ![]() .
.
其中可作为该平面其他向量基底的是( )
A.①②
B.①③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 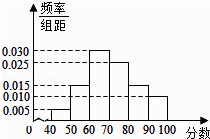
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品在某销售点的零售价x(单位:元)与每天的销售量y(单位:个)的统计数据如表所示:
x | 16 | 17 | 18 | 19 |
y | 50 | 34 | 41 | 31 |
由表可得回归直线方程 ![]() 中的
中的 ![]() ,根据模型预测零售价为20元时,每天的销售量约为( )
,根据模型预测零售价为20元时,每天的销售量约为( )
A.30
B.29
C.27.5
D.26.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() ﹣
﹣ ![]() =1表示焦点在y轴上的椭圆;命题q:双曲线
=1表示焦点在y轴上的椭圆;命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
=1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点. 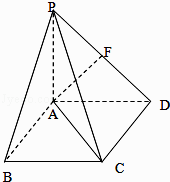
(1)求证:AF⊥平面PDC;
(2)求直线AC与平面PCD所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com