
【题目】已知直线y=﹣x+1与椭圆 ![]() +
+ ![]() =1(a>b>0)相交于A、B两点,且线段AB的中点在直线l:x﹣2y=0上,求此椭圆的离心率.
=1(a>b>0)相交于A、B两点,且线段AB的中点在直线l:x﹣2y=0上,求此椭圆的离心率.
【答案】解:联立直线y=﹣x+1与直线l:x﹣2y=0,得x= ![]() ,y=
,y= ![]() , ∴直线y=﹣x+1与x﹣2y=0的交点为M(
, ∴直线y=﹣x+1与x﹣2y=0的交点为M( ![]() ,
, ![]() ),∴线段AB的中点为(
),∴线段AB的中点为( ![]() ,
, ![]() ),
),
设y=﹣x+1与 ![]() +
+ ![]() =1的交点分别为A(x1 , y1),B(x2 , y2),
=1的交点分别为A(x1 , y1),B(x2 , y2),
则x1+x2= ![]() ,y1+y2=
,y1+y2= ![]() ,
,
分别把A(x1 , y1),B(x2 , y2)代入椭圆 ![]() +
+ ![]() =1(a>b>0),
=1(a>b>0),
两式相减,得﹣ ![]() =﹣
=﹣ ![]() ,
,
∴a2=2b2 , ∴a= ![]() b=
b= ![]() c,∴e=
c,∴e= ![]()
【解析】联立直线y=﹣x+1与直线l:x﹣2y=0得到线段AB的中点为( ![]() ,
, ![]() ),设y=﹣x+1与
),设y=﹣x+1与 ![]() +
+ ![]() =1的交点分别为A(x1 , y1),B(x2 , y2),利用点差法能求出椭圆的离心率.
=1的交点分别为A(x1 , y1),B(x2 , y2),利用点差法能求出椭圆的离心率.


科目:高中数学 来源: 题型:
【题目】已知函数f(x),定义 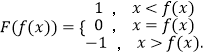
(Ⅰ)写出函数F(2x﹣1)的解析式;
(Ⅱ)若F(|x﹣a|)+F(2x﹣1)=0,求实数a的值;
(Ⅲ)当 ![]() 时,求h(x)=cosxF(x+sinx)的零点个数和值域.
时,求h(x)=cosxF(x+sinx)的零点个数和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下面四个命题: (1.)从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样;
(2.)两个随机变量相关性越强,则相关系数的绝对值越接近于1;
(3.)对分类变量X和Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大;
(4.)在回归直线方程 ![]() =0.4x+12中,当解释变量x每增加一个单位时,预报变量大约增加0.4个单位.
=0.4x+12中,当解释变量x每增加一个单位时,预报变量大约增加0.4个单位.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上. (Ⅰ)求异面直线D1E与A1D所成的角;
(Ⅱ)若二面角D1﹣EC﹣D的大小为45°,求点B到平面D1EC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元.甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1小时、2小时,加工一件乙产品所需工时分别为2小时、1小时,A、B两种设备每月有效使用台时数分别为400小时和500小时.如何安排生产可使月收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com