
【题目】函数f(x)=log2(x+2)的定义域是( )
A.[2,+∞)
B.[﹣2,+∞)
C.(﹣2,+∞)
D.(﹣∞,﹣2)
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1 , S2 , S4成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品在某销售点的零售价x(单位:元)与每天的销售量y(单位:个)的统计数据如表所示:
x | 16 | 17 | 18 | 19 |
y | 50 | 34 | 41 | 31 |
由表可得回归直线方程 ![]() 中的
中的 ![]() ,根据模型预测零售价为20元时,每天的销售量约为( )
,根据模型预测零售价为20元时,每天的销售量约为( )
A.30
B.29
C.27.5
D.26.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() ﹣
﹣ ![]() =1表示焦点在y轴上的椭圆;命题q:双曲线
=1表示焦点在y轴上的椭圆;命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
=1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(0)=0,f(x)+f(1﹣x)=1,f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )等于( )
)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 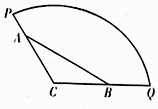
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在射线y=2x﹣3(x≥0),且与直线y=x+2和y=﹣x+4都相切.
(1)求圆C的方程;
(2)若P(x,y)是圆C上任意一点,求x+2y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com