
【题目】定义在R上的函数f(x)满足f(0)=0,f(x)+f(1﹣x)=1,f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )等于( )
)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵f(0)=0,f(x)+f(1﹣x)=1,令x=1得:f(1)=1, 又f( ![]() )=
)= ![]() f(x),
f(x),
∴当x=1时,f( ![]() )=
)= ![]() f(1)=
f(1)= ![]() ;
;
令x= ![]() ,由f(
,由f( ![]() )=
)= ![]() f(x)得:
f(x)得:
f( ![]() )=
)= ![]() f(
f( ![]() )=
)= ![]() ;
;
同理可求:f( ![]() )=
)= ![]() f(
f( ![]() )=
)= ![]() ;
;
f( ![]() )=)=
)=)= ![]() f(
f( ![]() )=
)= ![]() ;
;
f( ![]() )=
)= ![]() f(
f( ![]() )=
)= ![]() ①
①
再令x= ![]() ,由f(x)+f(1﹣x)=1,可求得f(
,由f(x)+f(1﹣x)=1,可求得f( ![]() )=
)= ![]() ,
,
∴f( ![]() )+f(1﹣
)+f(1﹣ ![]() )=1,解得f(
)=1,解得f( ![]() )=
)= ![]() ,
,
令x= ![]() ,同理反复利用f(
,同理反复利用f( ![]() )=
)= ![]() f(x),
f(x),
可得f( ![]() )=)=
)=)= ![]() f(
f( ![]() )=
)= ![]() ;
;
f( ![]() )=
)= ![]() f(
f( ![]() )=
)= ![]() ;
;
…
f( ![]() )=
)= ![]() f(
f( ![]() )=
)= ![]() ②
②
由①②可得:,有f( ![]() )=f(
)=f( ![]() )=
)= ![]() ,
,
∵0≤x1<x2≤1时f(x1)≤f(x2),而0< ![]() <
< ![]() <
< ![]() <1
<1
所以有f( ![]() )≥f(
)≥f( ![]() )=
)= ![]() ,
,
f( ![]() )≤f(
)≤f( ![]() )=
)= ![]() ;
;
故f( ![]() )=
)= ![]() .
.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°, ![]() ,D为AC上一点,且AD=3DC.
,D为AC上一点,且AD=3DC. 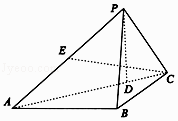
(1)求证:PD⊥平面ABC;
(2)若E为PA中点,求直线CE与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N. 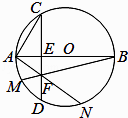
(1)求证:B、E、F、N四点共圆;
(2)求证:AC2+BFBM=AB2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元.甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1小时、2小时,加工一件乙产品所需工时分别为2小时、1小时,A、B两种设备每月有效使用台时数分别为400小时和500小时.如何安排生产可使月收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com