
【题目】已知数列{an}的前n项和为 ![]() ,{bn}为等差数列,且b1=4,b3=10,则数列
,{bn}为等差数列,且b1=4,b3=10,则数列 ![]() 的前n项和Tn= .
的前n项和Tn= .
【答案】n×2n+2
【解析】解:∵数列{an}的前n项和为 ![]() ,
,
∴a1=S1=3+8=11,
an=Sn﹣Sn﹣1=(3n2+8n)﹣[3(n﹣1)2+8(n﹣1)]=6n+5,
n=1时,上式成立,
∴an=6n+5.
∵{bn}为等差数列,且b1=4,b3=10,
∴b3=4+2d=10,解得d=3,
∴bn=4+(n﹣1)×3=3n+1,
∴ ![]() =
= ![]() =(n+1)2n+1,
=(n+1)2n+1,
∴数列 ![]() 的前n项和:
的前n项和:
Tn=2×22+3×23+4×24+…+(n+1)×2n+1,①
2Tn=2×23+3×24+4×25+…+(n+1)×2n+2,②
①﹣②,得:
﹣Tn=8+23+24+…+2n+1﹣(n+1)×2n+2
=8+ ![]() ﹣(n+1)×2n+2
﹣(n+1)×2n+2
=﹣n×2n+2.
∴Tn=n×2n+2.
故答案为:n×2n+2.
推导出an=6n+5,bn=3n+1,从而 ![]() =
= ![]() =(n+1)2n+1,由此利用错位相减法能求出数列
=(n+1)2n+1,由此利用错位相减法能求出数列 ![]() 的前n项和.
的前n项和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域为{x|﹣2≤x≤3,且x≠2},值域为{y|﹣1≤y≤2,且y≠0},则y=f(x)的图象可能是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(0)=0,f(x)+f(1﹣x)=1,f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )等于( )
)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() +
+ ![]() )
) ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈(0, ![]() )时,求函数f(x)的值域.
)时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 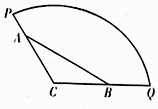
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( ) 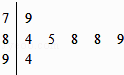
A.86.5,86.7
B.88,86.7
C.88,86.8
D.86,5,86.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an},{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com