
【题目】如图,在三棱锥P﹣ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°, ![]() ,D为AC上一点,且AD=3DC.
,D为AC上一点,且AD=3DC. 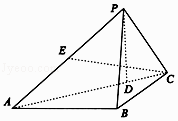
(1)求证:PD⊥平面ABC;
(2)若E为PA中点,求直线CE与平面PAB所成角的正弦值.
【答案】
(1)证明:取AC中点O,连接OP,OB,
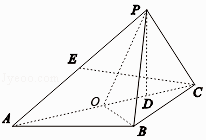
则由AD=3DC,知D为OC中点.
∵AB=BC=2,∠ABC=120°,
∴由余弦定理,得 ![]() .
.
∵PA⊥PC,∴在Rt△PAC中, ![]() ,
,
∴OP=PC,∴PD⊥AC.
又∵PB=AB=BC=2,∴OB⊥AC, ![]() ,∴OB2+OP2=PB2,∴OB⊥OP,
,∴OB2+OP2=PB2,∴OB⊥OP,
又∵OP∩AC=O,∴OB⊥平面PAC,∵PD平面PAC,∴OB⊥PD,
又∵OB∩AC=O,∴PD⊥平面ABC.
(2)解:以O为坐标原点,OA,OB所在直线分别为x,y轴,建立空间直角坐标系O﹣xyz,如图所示,
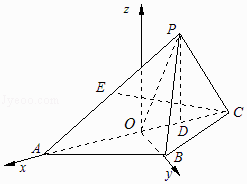
则 ![]() ,B(0,1,0),
,B(0,1,0), ![]() ,
, ![]() ,
, ![]() ,∴
,∴ ![]() ,
, ![]() ,
, ![]() .
.
设 ![]() 是平面PAB的一个法向量,则
是平面PAB的一个法向量,则
由 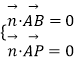 ,得
,得 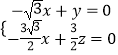 ,取x=1,则
,取x=1,则 ![]() .
.
设直线CE与平面PAB所成角为θ,则 ![]() ,
,
∴直线CE与平面PAB所成角的正弦值为 ![]() .
.
解法二:作EF⊥AC于F,则 ![]() ,
, ![]() ,
,
所以 ![]() .在△PAB中,AB=PB=2,
.在△PAB中,AB=PB=2, ![]() ,
,
所以高 ![]()
设点C到平面PAB的距离为h,则 ![]()
另一方面, ![]()
所以 ![]() ,
,
所以直线CE与平面PAB所成角的正弦值 ![]() .
.
【解析】(1)取AC中点O,连接OP,OB,证明PD⊥AC,OB⊥PD,利用线面垂直的判定定理,证明PD⊥平面ABC;(2)方法一:以O为坐标原点,OA,OB所在直线分别为x,y轴,建立空间直角坐标系,求出平面的法向量,利用向量方法求直线CE与平面PAB所成角的正弦值.方法二:作EF⊥AC于F,求出点C到平面PAB的距离,即可求直线CE与平面PAB所成角的正弦值.
【考点精析】利用直线与平面垂直的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则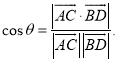 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点. 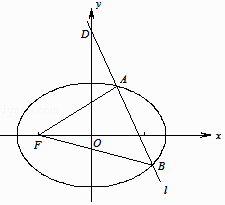
(1)求椭圆C的方程;
(2)是否存在定点 ![]() ,使
,使 ![]()
![]() 恒为定值.若存在求出这个定值;若不存在,说明理由.
恒为定值.若存在求出这个定值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点
=1(a>b>0)的左右焦点分别为F1 , F2 , 抛物线y2=4x与椭圆C有相同的焦点,且椭圆C过点 ![]() . (I)求椭圆C的标准方程;
. (I)求椭圆C的标准方程;
(Ⅱ)若椭圆C的右顶点为A,直线l交椭圆C于E、F两点(E、F与A点不重合),且满足AE⊥AF,若点P为EF中点,求直线AP斜率的最大值.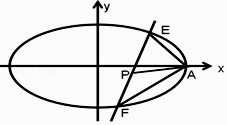
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(0)=0,f(x)+f(1﹣x)=1,f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )等于( )
)等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() +
+ ![]() )
) ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈(0, ![]() )时,求函数f(x)的值域.
)时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市举办青少年运动会上,7位裁判为某武术队员打出的分数的茎叶图,左边数字表示十位数字,右边数字表示个位数字,这些数据的中位数是( ),去掉一个最低分和最高分所剩数据的平均数是( ) 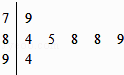
A.86.5,86.7
B.88,86.7
C.88,86.8
D.86,5,86.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷等差数列{an}的前n项和为Sn , 已知a1=1,S3=12.
(1)求a24与S7的值;
(2)已知m、n均为正整数,满足am=Sn . 试求所有n的值构成的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com