练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求证：（1-tanα）=（cos2α-cotα）（sec2α+tanα）．

    解：等式左边：（1-tanα）=．．
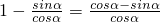
    等式的右边（cos2α-cotα）（sec2α+tanα）==．
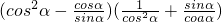
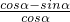
    所以左边等于右边，
    故（1-tanα）=（cos2α-cotα）（sec2α+tanα）成立．
    分析：首先要证明等式（1-tanα）=（cos2α-cotα）（sec2α+1tanα），就必须了解各种三角函数之间的转化关系，然后把它们都换成正余弦函数的形式，再求证．
    点评：此题主要考查三角函数恒等式的证明问题，其中运用到各种三角函数间的转化关系，在做题的时候要把它们转化统一再求证．属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    求证：
    1+sinα
    1-2sin2
    α
    2
    =
    1+tan
    α
    2
    1-tan
    α
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求证：
    		3
    tan 18°+tan 18°•    tan 12°+
    		3
    tan 12°=1    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求证：（sinα+tanα）（cosα+cotα）=（1+sinα）（1+cosα）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (1)求证：（1+tan）;

    (2)已知=1,求证：tan2θ=tanα·tanβ.

    查看答案和解析>>

    同步练习册答案