
 ,则
,则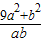 的最大值与最小值之和为( )
的最大值与最小值之和为( )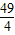
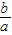 表示区域内一点与原点连线的斜率,可得出1≤
表示区域内一点与原点连线的斜率,可得出1≤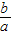 ≤4,再将
≤4,再将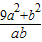 表示成关于
表示成关于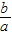 的函数,即可算出
的函数,即可算出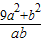 的最大值与最小值,进而得到本题的答案.
的最大值与最小值,进而得到本题的答案.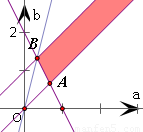 以a为横坐标,b为纵坐标建立如图直角坐标系,
以a为横坐标,b为纵坐标建立如图直角坐标系,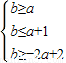 表示的平面区域,
表示的平面区域, ,
, ),B(
),B( ,
, )
)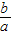 表示区域内一点P与原点连线的斜率
表示区域内一点P与原点连线的斜率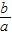 达到最小值1;当P点与B点重合时,
达到最小值1;当P点与B点重合时, 达到最大值4
达到最大值4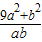 =
=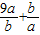 ≥2
≥2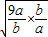 =6,当且仅当
=6,当且仅当 =3时取等号;
=3时取等号;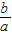 =1时,
=1时, 有最大值10
有最大值10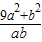 的最大值为10,最小值为6.可得最大值与最小值之和等于16
的最大值为10,最小值为6.可得最大值与最小值之和等于16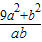 的最值,着重考查了二元一次不等式表示的平面区域、直线的斜率和简单的线性规划等知识,属于基础题.
的最值,着重考查了二元一次不等式表示的平面区域、直线的斜率和简单的线性规划等知识,属于基础题. 

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com