练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设抛物线的焦点为，准线为，为过焦点且垂直于轴的抛物线的弦，已知以为直径的圆经过点.

    （1）求的值及该圆的方程；

    （2）设为上任意一点，过点作的切线，切点为，证明：.

    【答案】（1），圆的方程为：.（2）答案见解析

    【解析】

    （1）根据题意，可知点的坐标为，即可求出的值，即可求出该圆的方程；

    （2）由题易知，直线的斜率存在且不为0，设的方程为，与抛物线联立方程组，根据，求得，化简解得，进而求得点的坐标为，分别求出，，利用向量的数量积为0，即可证出.

    解：（1）易知点的坐标为，

    所以，解得.

    又圆的圆心为，

    所以圆的方程为.

    （2）证明易知，直线的斜率存在且不为0，

    设的方程为，

    代入的方程，得.

    令，得，

    所以，解得.

    将代入的方程，得，即点的坐标为.

    所以，，

    .

    故.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知

    (1)求函数的极值；

    (2)设，对于任意，总有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中错误的是（ ）

    A. 命题“若，则”的逆否命题是真命题

    B. 命题“”的否定是“”

    C. 若为真命题，则为真命题

    D. 已知，则“”是“”的必要不充分条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的参数方程为（为参数），以直角坐标系的原点o为极点，x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程是：

    （Ⅰ）求曲线C的普通方程和直线l的直角坐标方程：

    （Ⅱ）点P是曲线C上的动点，求点P到直线l距离的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学使用某品牌暖水瓶，其内胆规格如图所示．若水瓶内胆壁厚不计，且内胆如图分为①②③④四个部分，它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱体．若其中圆台部分的体积为，且水瓶灌满水后盖上瓶塞时水溢出．记盖上瓶塞后，水瓶的最大盛水量为，

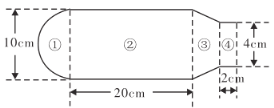
    （1）求；

    （2）该同学发现：该品牌暖水瓶盛不同体积的热水时，保温效果不同．为了研究保温效果最好时暖水瓶的盛水体积，做以下实验：把盛有最大盛水量的水的暖水瓶倒出不同体积的水，并记录水瓶内不同体积水在不同时刻的水温，发现水温（单位：℃）与时刻满足线性回归方程，通过计算得到下表：

    倒出体积

    0

    30

    60

    90

    120

    拟合结果

    倒出体积

    150

    180

    210

    …

    450

    拟合结果

    …

    注：表中倒出体积（单位：）是指从最大盛水量中倒出的那部分水的体积．其中：

    令．对于数据，可求得回归直线为，对于数据，可求得回归直线为．

    （ⅰ）指出的实际意义，并求出回归直线的方程（参考数据：）；

    （ⅱ）若与的交点横坐标即为最佳倒出体积，请问保温瓶约盛多少体积水时（盛水体积保留整数，且取3.14）保温效果最佳？

    附：对于一组数据，其回归直线中的斜率和截距的最小二乘估计分别为．

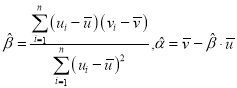    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （Ⅰ）求直线的普通方程和曲线的直角坐标方程；

    （Ⅱ）设为曲线上的点，，垂足为，若的最小值为，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： （a>b>0），四点P1（1,1），P2（0,1），P3（–1， ），P4（1， ）中恰有三点在椭圆C上.

    （1）求C的方程；

    （2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）讨论的单调性；

    （2）设，若在上恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着马拉松运动在全国各地逐渐兴起，参与马拉松训练与比赛的人数逐年增加．为此，某市对参加马拉松运动的情况进行了统计调査，其中一项是调査人员从参与马拉松运动的人中随机抽取100人，对其每月参与马拉松运动训练的夭数进行统计，得到以下统计表；

    平均每月进行训练的天数

    人数

    15

    60

    25

    （1）以这100人平均每月进行训练的天数位于各区间的频率代替该市参与马拉松训练的人平均每月进行训练的天数位于该区间的概率．从该市所有参与马拉松训练的人中随机抽取4个人，求恰好有2个人是“平均每月进行训练的天数不少于20天”的概率；

    （2）依据统计表，用分层抽样的方法从这100个人中抽取12个，再从抽取的12个人中随机抽取3个，表示抽取的是“平均每月进行训练的天数不少于20天”的人数，求的分布列及数学期望

    查看答案和解析>>

    同步练习册答案