
分析 (1)直接利用余弦定理化简已知条件,然后求角A的余弦函数值,即可求解;
(2)由已知利用余弦定理可得c2-4c+1=0,即可解得c的值.
解答 解:(1)在△ABC中,角A、B、C的对边分别为a、b、c,若$\frac{c}{2}$=b-acosC=b-a$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
可得2b2-bc=a2+b2-c2,即c2+b2-bc=a2,又由余弦定理c2+b2-2bccosA=a2,
∴cosA=$\frac{1}{2}$,
∴A=60°.
(2)∵a=$\sqrt{15}$,b=4,A=60°,
∴由余弦定理a2=b2+c2-2bccosA,可得:15=16+c2-2×$4×c×\frac{1}{2}$,整理可得:c2-4c+1=0,
∴解得:c=2±$\sqrt{3}$.
点评 本题考查余弦定理在解三角形中的应用,考查分析问题解决问题的能力,考查了转化思想,属于基础题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x=3或y=1} | B. | {3,1} | C. | {(3,1)} | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{13}$ | B. | $\frac{5}{7}$ | C. | $\frac{17}{25}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
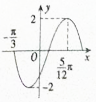 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com