
分析 (1)利用特征值与特征向量的定义,建立方程组,即可求得A;
(2)求出|A|,即可求得逆矩阵A-1.
解答 解:(1)设A=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$,则
∵二阶矩阵A有特征值λ1=3及其对应的一个特征向量$\overrightarrow{a}$1=$[\begin{array}{l}{1}\\{1}\end{array}]$,特征值λ2=-1及其对应的一个特征向量$\overrightarrow{a}$2=$[\begin{array}{l}{1}\\{-1}\end{array}]$,
∴$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=3$[\begin{array}{l}{1}\\{1}\end{array}]$,$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{1}\\{-1}\end{array}]$=-$[\begin{array}{l}{1}\\{-1}\end{array}]$,
∴$\left\{\begin{array}{l}{a+b=3}\\{c+d=3}\end{array}\right.$且$\left\{\begin{array}{l}{a-b=-1}\\{c-d=1}\end{array}\right.$,
∴a=1,b=2,c=2,d=1,
∴A=$[\begin{array}{l}{1}&{2}\\{2}&{1}\end{array}]$;
(2)|A|=1-4=-3,
∴A-1=$[\begin{array}{l}{-\frac{1}{3}}&{\frac{2}{3}}\\{\frac{2}{3}}&{-\frac{1}{3}}\end{array}]$.
点评 本题主要考查了二阶矩阵,以及特征值与特征向量的计算,考查逆矩阵,正确理解特征值与特征向量是关键,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
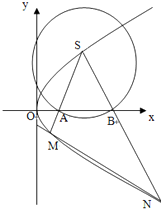 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com