
分析 (1)对g(x)在[2,3]上的单调性进行讨论列方程组解出.
(2)令|2x-1|=t,则f(|2x-1|)+k($\frac{2}{|{2}^{x}-1|}$-3)=0有三个不同的解?t2-(2+3k)t+1+2k=0的两根分别在(0,1)和(1,+∞)上.
解答 解:(1)∵a≠0,∴g(x)的对称轴为x=1,∴g(x)在[2,3]上是单调函数,
∴$\left\{\begin{array}{l}{g(2)=1}\\{g(3)=4}\end{array}\right.$,或$\left\{\begin{array}{l}{g(2)=4}\\{g(3)=1}\end{array}\right.$,解得a=1,b=0,或a=-1.b=3(舍).
∴a=1,b=0.
(2)f(x)=$\frac{{x}^{2}-2x+1}{x}$=x+$\frac{1}{x}$-2.
令|2x-1|=t,显然t>0,∴t+$\frac{1}{t}$-2+k($\frac{2}{t}-3$)=0在(0,1)上有一解,在[1,+∞)上有一解.
即t2-(2+3k)t+1+2k=0的两根分别在(0,1)和[1,+∞)上.令h(t)=t2-(2+3k)t+1+2k,
若h(1)=0,即1-2-3k+1+2k=0,解得k=0,则h(t)=t2-2t+1=(t-1)2,与h(t)有两解矛盾.
∴$\left\{\begin{array}{l}{h(0)>0}\\{h(1)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{1+2k>0}\\{-k<0}\end{array}\right.$,解得k>0,
∴实数k的取值范围是(0,+∞).
点评 本题考查了二次函数的单调性,零点范围与系数的关系,属于中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,2$\sqrt{2}$) | C. | (3,2$\sqrt{3}$) | D. | (4,±4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
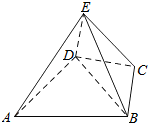 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com