
分析 先利用矩阵的乘法公式求出MN,由此能利用矩阵的初等变换能求出矩阵MN的逆矩阵.
解答 解:∵矩阵M=$[\begin{array}{l}{3}&{0}\\{0}&{1}\end{array}]$,N=$[\begin{array}{l}{1}&{0}\\{0}&{\frac{1}{2}}\end{array}]$,
∴MN=$[\begin{array}{l}{3}&{0}\\{0}&{1}\end{array}]$$[\begin{array}{l}{1}&{0}\\{0}&{\frac{1}{2}}\end{array}]$=$[\begin{array}{l}{3}&{0}\\{0}&{\frac{1}{2}}\end{array}]$,
∵$[\begin{array}{l}{3}&{0}&{\;}&{1}&{0}\\{0}&{\frac{1}{2}}&{\;}&{0}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{\;}&{\frac{1}{3}}&{0}\\{0}&{\frac{1}{2}}&{\;}&{0}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{\;}&{\frac{1}{3}}&{0}\\{0}&{1}&{\;}&{0}&{2}\end{array}]$,
∴矩阵MN的逆矩阵是$[\begin{array}{l}{\frac{1}{3}}&{0}\\{0}&{2}\end{array}]$.
故答案为:$[\begin{array}{l}{\frac{1}{3}}&{0}\\{0}&{2}\end{array}]$.
点评 本题考查两个矩阵乘积的逆矩阵的求法,是中档题,解题时要认真审题,注意矩阵的乘法公式和矩阵的初等变换的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | $-\frac{π}{4}$ | $\frac{π}{12}$ | $\frac{5π}{12}$ | $\frac{3π}{4}$ | $\frac{13π}{12}$ |
| ωx+ϕ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x) | 2 | 6 | 2 | -2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
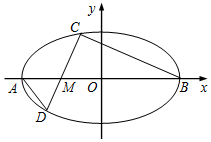 在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,两个顶点分别为A(-a,0),B(a,0),点M(-1,0),且3$\overrightarrow{AM}$=$\overrightarrow{MB}$,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.
在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,两个顶点分别为A(-a,0),B(a,0),点M(-1,0),且3$\overrightarrow{AM}$=$\overrightarrow{MB}$,过点M斜率为k(k≠0)的直线交椭圆E于C,D两点,其中点C在x轴上方.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{7}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | $\frac{5}{2}$ | D. | $\frac{\sqrt{10}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-5y-11=0 | B. | 5x-3y-13=0 | C. | 5x+3y-7=0 | D. | 3x+5y-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com