解:(Ⅰ)设等比数列{a
n}的公比为q,
则q>0且
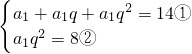
,
①÷②得:
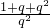
=

,整理得:3q
2-4q-4=0,
解得:q=-

(舍去),q=2,∵a
1=2,∴a
n=2
n(n∈N
+);
(Ⅱ)当n=1时,
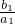
=

,a
1=2,∴b
1=1,
当n≥2时,
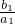
+
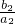
+…+

=

①,
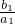
+
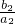
+…+
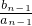
=
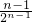
②(n∈N
*),
①-②得:

=

-
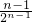
=
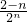
,又a
n=2
n,
∴b
n=2-n(n≥2),又∵b
1=1=2-1,∴b
n=2-n(n∈N
+),
∵b
n+1-b
n=-1,
∴数列{b
n}是以1为首项,-1为公差的等差数列.
分析:(Ⅰ)设出等比数列{a
n}的公比为q,根据a
3=8,前3项的和S
3=14,列出关于首项和公比的方程组,消去首项得到关于q的方程,求出方程的解即可得到q的值,进而求出首项的值,根据首项和公比写出数列{a
n}的通项公式即可;
(Ⅱ)令n=1代入已知的等式中,由a
1的值求出b
1的值,然后当n≥2时,已知的等式记作①,把n换为n-1得到另一个等式,记作②,①-②且由(Ⅰ)求出的a
n的通项公式即可得到b
n的通项公式,把b
1的值代入也满足,利用b
n+1-b
n即可求出数列的公差,进而推出数列{b
n}是等差数列,得证.
点评:此题考查学生灵活运用等比数列的通项公式化简求值,掌握等差数列的确定方法,是一道中档题.学生在第二问中求出b
n的通项公式后要注意把b
1的值代入进行验证.

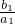 +
+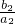 +…+
+…+ =
= (n∈N*),证明:{bn}是等差数列.
(n∈N*),证明:{bn}是等差数列.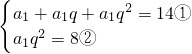 ,
,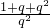 =
= ,整理得:3q2-4q-4=0,
,整理得:3q2-4q-4=0, (舍去),q=2,∵a1=2,∴an=2n(n∈N+);
(舍去),q=2,∵a1=2,∴an=2n(n∈N+);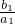 =
= ,a1=2,∴b1=1,
,a1=2,∴b1=1,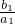 +
+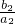 +…+
+…+ =
= ①,
①,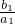 +
+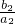 +…+
+…+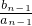 =
=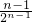 ②(n∈N*),
②(n∈N*), =
= -
-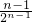 =
=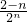 ,又an=2n,
,又an=2n,
