
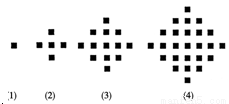
(本题满分12分)某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出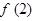 ,
,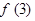
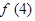
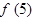 并猜测
并猜测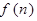 的表达式;
的表达式;
(2)求证:+++…+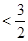 .
.
解: (1)∵ f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴ f(5)=25+4×4=41.
∵ f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
f(n)=2n2-2n+1.
(2)当n≥2时,==,
∴ +++…+
=1+
=1+=- .
.
【解析】本试题主要是考查了数列的归纳猜想思想的运用,根据前几项。来猜想并运用数学归纳法加以证明。
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论。
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可。
解: (1)∵ f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴ f(5)=25+4×4=41.
∵ f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n. ∴ f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,
∴ f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴ f(n)=2n2-2n+1(n≥2),
又n=1时,f(1)也适合f(n).
∴ f(n)=2n2-2n+1. --------6分
(2)当n≥2时,==,
∴ +++…+[来源:Z,xx,k.Com]
=1+
=1+=- . ---------------12分
. ---------------12分


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
(本题满分12分)
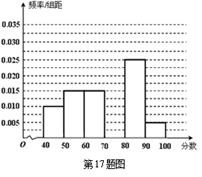
某校从参加高一年级期中考试的学生中随机抽出![]() 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)若从![]() 名学生中随机抽取
名学生中随机抽取![]() 人,抽到的学生成绩在
人,抽到的学生成绩在![]() 记
记![]() 分,在
分,在![]() 记
记![]() 分,在
分,在![]() 记
记![]() 分,用
分,用![]() 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2011届四川省南充市高三适应性考试数学理卷 题型:解答题
(本题满分12分)
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5,且相互之间无影响.
(1)求至少3个员工同时上网的概率;
(2)求至少几个员工同时上网的概率小于0.3?
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:
 ,
, ,…,
,…, 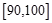 后得到如下频率分布直方图.
后得到如下频率分布直方图.

(Ⅰ)求分数在 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人, 求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源:2014届云南省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)某厂生产 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套 型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套
型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时。厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时。已知该厂生产一套 型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产
型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产 两型会议桌多少套,才能获得最大利润?最大利润是多少?
两型会议桌多少套,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源:2010年陕西省高二上学期期中考试数学理卷 题型:解答题
(本题满分12分)某学校校办工厂有毁坏的房屋一座,留有一面14m的旧墙,现准备利用这面墙的一段为面墙,建造平面图形为矩形且面积为126 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是:
(1)修1m旧墙的费用是造1m新墙费用的25%;
(2)拆去1m旧墙用所得的材料来建1m新墙的费用是建1m新墙费用的50%.
问如何利用旧墙才能使建墙的费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com