
已知二次函数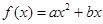 满足条件:
满足条件:
①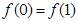 ;②
;②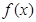 的最小值为
的最小值为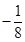 。
。
(1)求函数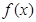 的解析式;
的解析式;
(2)设数列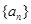 的前
的前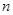 项积为
项积为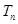 ,且
,且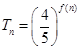 ,求数列
,求数列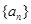 的通项公式;
的通项公式;
(3)在(2)的条件下,若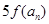 是
是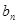 与
与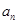 的等差中项,试问数列
的等差中项,试问数列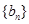 中第几项的值最小?求出这个最小值。
中第几项的值最小?求出这个最小值。
(Ⅰ)  . (Ⅱ)
. (Ⅱ) 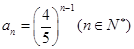 .
.
(3) 即数列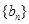 中
中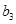 最小, 且
最小, 且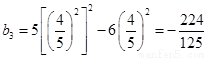 .
.
【解析】题考查了二次函数的解析式的求解,以及数列的递推关系,数列的求和问题,属于中档题,同时也考查了学生的计算能力.
(1)函数的待定系数法,以及函数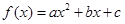 在
在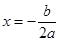 处取得最值的方法,求得待定系数,确定函数解析式;(2)类比
处取得最值的方法,求得待定系数,确定函数解析式;(2)类比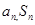 之间的关系,
之间的关系,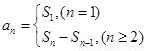 ,数列
,数列 的前
的前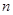 项积为
项积为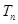 则
则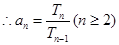 ,从而求解;
,从而求解;
(3)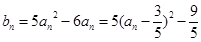 需判断
需判断 的单调性,考察分类讨论思想。
的单调性,考察分类讨论思想。
解: (Ⅰ)题知: 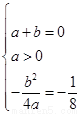 ,
解得
,
解得 ,
,
故 . ……3分
. ……3分
(Ⅱ)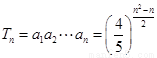 ,
,
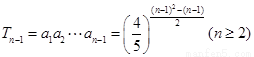 ,
,
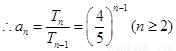 , 又
, 又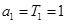 满足上式. 所以
满足上式. 所以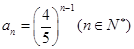 .
.
(3) 若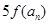 是
是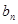 与
与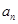 的等差中项, 则
的等差中项, 则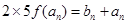 ,
,
从而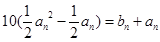 , 得
, 得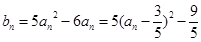 . ……9分
. ……9分
因为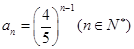 是
是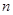 的减函数, 所以
的减函数, 所以
当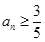 , 即
, 即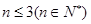 时,
时, 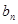 随
随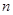 的增大而减小, 此时最小值为
的增大而减小, 此时最小值为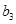 ;
;
当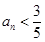 , 即
, 即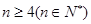 时,
时, 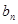 随
随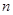 的增大而增大, 此时最小值为
的增大而增大, 此时最小值为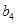 . ……13分
. ……13分
又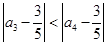 , 所以
, 所以 ,
,
即数列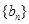 中
中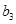 最小, 且
最小, 且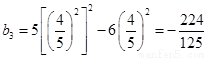 .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
(09年华师一附中期中检测文)(12分)
已知二次函数![]() 满足条件:
满足条件:
①对任意![]() ,均有
,均有![]() ;②函数
;②函数![]() 的图象与直线
的图象与直线![]() 相切
相切
(I)求函数![]() 的解析式;
的解析式;
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数![]() 满足条件
满足条件![]() ,且方程
,且方程![]() 有等根。
有等根。
(1)求函数![]() 的解析式;
的解析式;
(2)是否存在实数![]() 使
使![]() 的定义域和值域分别为
的定义域和值域分别为![]() 和
和![]() ,如果存在,求出
,如果存在,求出![]() 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分15分)已知二次函数![]() 满足条件:①
满足条件:① ![]() ; ②
; ② ![]() 的最小值为
的最小值为![]() .
.
(1) 求函数![]() 的解析式; (2) 设数列
的解析式; (2) 设数列![]() 的前
的前![]() 项积为
项积为![]() , 且
, 且![]() , 求数列
, 求数列![]() 的通项公式; (3) 在(2)的条件下, 求数列
的通项公式; (3) 在(2)的条件下, 求数列![]() 的前
的前![]() 项的和.
项的和.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高一10月月考数学试卷(解析版) 题型:解答题
(本小题满分12分) 已知二次函数 满足条件
满足条件 ,及
,及 .
.
(1)求 的解析式;(2)求
的解析式;(2)求 在
在 上的最大和最小值.
上的最大和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com