
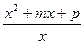 ,(p≠0)是奇函数.
,(p≠0)是奇函数.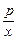 +m=-x-
+m=-x-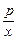 -m.∴2m=0.∴m=0.
-m.∴2m=0.∴m=0. ,所以f’(x)="1-p/x2," 当p>0时,
,所以f’(x)="1-p/x2," 当p>0时,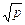 或x>
或x>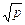
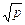 <x<0或0<x<
<x<0或0<x<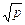
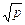 )上是减函数,在(
)上是减函数,在(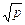 ,+∞)上是增函数.
,+∞)上是增函数.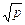 ∈[1,2]时,f(x)在[1,p]上是减函数.在[p,2]上是增函数.
∈[1,2]时,f(x)在[1,p]上是减函数.在[p,2]上是增函数.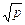 )=2
)=2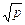 .
.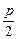 }.
}.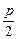 ,f(x)max=f(2);当2<p≤4时,1+p≥2+
,f(x)max=f(2);当2<p≤4时,1+p≥2+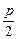 ,f(x)max=f(1).
,f(x)max=f(1).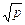 >2,即p>4时,f(x)在[1,2]上为减函数,
>2,即p>4时,f(x)在[1,2]上为减函数,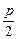 .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:不详 题型:单选题
| A.10×210 | B.10×210+1 | C.10×210+2 | D.10×210-1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
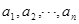 (
(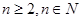 ).定义如下操作过程T:从A中任取两项
).定义如下操作过程T:从A中任取两项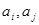 ,将
,将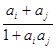 的值添在A的最后,然后删除
的值添在A的最后,然后删除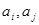 ,这样得到一系列
,这样得到一系列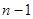 项的新数列A1(约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列
项的新数列A1(约定:一个数也视作数列);对A1的所有可能结果重复操作过程T又得到一系列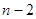 项的新数列A2,如此经过
项的新数列A2,如此经过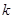 次操作后得到的新数列记作Ak .设A:
次操作后得到的新数列记作Ak .设A: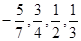 ,则A3的可能结果是……………………………( )
,则A3的可能结果是……………………………( )| A.0; | B.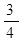 ; ; | C.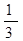 ; ; | D.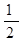 . . |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
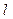 使得直线
使得直线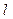 上任一点在映射f的作用下,仍在直线上,若存在求出的
上任一点在映射f的作用下,仍在直线上,若存在求出的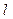 方程,若不存在说明理由.
方程,若不存在说明理由. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com