
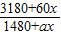 (1≤x≤10).(6分)
(1≤x≤10).(6分)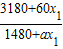 -
-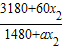 =
=
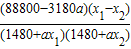 .
.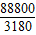 ≈27.9.又∵a∈N*,∴a=27.
≈27.9.又∵a∈N*,∴a=27.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)沿海地区某农村在2010年底共有人口1480人,全年工农业生产总值为3180万,从2011年起计划10年内该村的总产值每年增加60万元,人口每年净增a人,设从2011年起的第x年(2011年为第一年)该村人均产值为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)为使该村的人均产值10年内每年都有增长,那么该村每年人口的净增不能超过多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com