练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，底面是边长为的正方形，侧棱底面，且侧棱的长是，点分别是的中点.

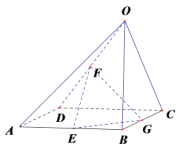
    （Ⅰ）证明： 平面；

    （Ⅱ）求三棱锥的体积.

    【答案】（Ⅰ）证明见解析；（Ⅱ） .

    【解析】试题分析：（Ⅰ）连结，通过勾股定理计算可知，由三线合一得出平面；（Ⅱ）根据中位线定理计算得出是边长为的正三角形，以为棱锥的底面，则为棱锥的高，代入棱锥的体积公式计算.

    试题解析：（Ⅰ）证明: 四边形是边长为的正方形， 是的中点,

    又侧棱底面, 面

    又

    是等腰三角形， 是的中点, .

    同理 是等腰三角形， 是的中点,

    面

    平面

    （Ⅱ）侧棱底面, 面

    由（Ⅱ）知： 平面,是三棱锥到平面的距离

    分别是的中点, ， ,

    四边形是边长为的正方形， 是的中点

    三角形是等边三角形

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，200），[220.240），
    [240，260），[260，280），[280，300）分组的频率分布直方图如图．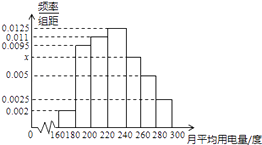

    （1）求直方图中x的值；
    （2）在月平均用电量为，[220，240），[240，260），[260，280）的三用户中，用分层抽样的方法抽取10居民，则月平均用电量在[220，240）的用户中应抽取多少户？
    （3）求月平均用电量的中位数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π，x∈R）在一个周期内的图象如图所示，则函数的解析式为 ． 直线y= 与函数y=f（x）（x∈R）图象的所有交点的坐标为 ．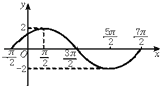

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的外接圆半径R= ，角A，B，C的对边分别是a，b，c，且 =
    （1）求角B和边长b；
    （2）求S△ABC的最大值及取得最大值时的a，c的值，并判断此时三角形的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年空气质量逐步雾霾天气现象增多，大气污染危害加重，大气污染可引起心悸，呼吸困难等心肺疾病，为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如下的列联表：

    患心肺疾病

    不患心肺疾病

    合计

    男

    5

    女

    10

    合计

    50

    已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为.

    （1）请将上面的列联表补充完整，并判断是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；

    （2）已知在患心肺疾病的10位女性中，有3位又患胃病，现在从患心肺疾病的10位女性中，选出3名进行其他方面的排查，记选出患胃病的女性人数为，求的分布列、数学期望及方差，下面的临界值表供参考：

    0.15

    0．10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式，其中.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的首项为8，Sn是其前n项的和，某同学经计算得S2=20，S3=36，S4=65，后来该同学发现了其中一个数算错了，则该数为（ ）
    A.S1
    B.S2
    C.S3
    D.S4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等比数列{an}的前n项和为Sn ， 已知S1 ， S3 ， S2成等差数列，
    （1）求{an}的公比q；
    （2）求a1﹣a3=3，求Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果右边程序执行后输出的结果是132，那么在程序until后面的“条件”应为( )

    A.i > 11
    B.i ≥11
    C.i ≤11
    D.i<11

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，直线过抛物线焦点，且与抛物线交于， 两点，以线段为直径的圆与抛物线准线的位置关系是（ ）

    A. 相离 B. 相交 C. 相切 D. 不确定

    查看答案和解析>>

    同步练习册答案