【答案】
分析:(1)若函数f(x)是增函数,则必要导数f'(x)≥0,由此不等式即可解出实数t的取值范围;
(2)由题意求证f(t)>13e
-2,可解出函数f(x)在区间[-2,+∞)上的最小值,由此最小值与13e
-2作比较即可证明此不等式;
(3)由题意先解出
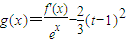
的解析式,由所得的解析式,及零点判定定理知,可研究此函数在区间(-2,t)两个端点值的符号及区间内函数最值的符号,由定理判断出零点个数即可
解答:解:(1)f(x)=(x
2-3x+3)e
x,f'(x)=(x
2-x)e
x=x(x-1)e
x,…(1分)
f'(x)≥0?x≥1或x≤0,…(2分)
若函数f(x)是定义域[-2,t]上的增函数,知t的取值范围是(-2,0].…(4分)
(2)由(1)知函数f(x)的增区间为[-2,0]与[1,+∞),减区间为[0,1],
从而函数f(x)在区间[-2,+∞)上有唯一的极小值f(1)=e,…(6分)
但f(-2)=13e
-2<e(∵
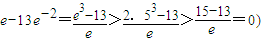
,
故函数f(x)在区间[-2,+∞)上的最小值为f(-2)=13e
-2,…(8分)
因为t>-2,所以f(t)>f(-2)=13e
-2.…(9分)
(3)
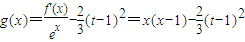
函数g(x)的图象是开口向上、对称轴为
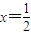
的抛物线,
且
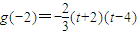
,
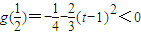
,
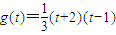
.
函数g(x)在区间(-2,t)内有两个零点
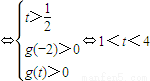
;…(9分)
当-2<t≤1时,g(-2)>0,g(t)≤0,又由
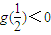
可知,函数g(x)在区间(-2,t)内只有一个零点;…(11分)
当t≥4时,g(-2)<0,g(t)>0,可知,函数g(x)在区间(-2,t)内只有一个零点.…(13分)
综上,当1<t<4时,函数g(x)在区间(-2,t)内有两个零点;
当-2<t≤1或t≥4时,函数g(x)在区间(-2,t)内只有一个零点.(14分)
点评:本题考查导数在最值问题中的运用,利用导数研究单调性,再利用单调性求最值,这是导数的重要运用,解答本题,第一小题关键是理解导数与函数单调性的关系,第二小题关键是将证明不等式问题转化为利用导数解出函数的最值,从而证明不等式,第三题解题的关键是理解零点定理及函数区间内函数最值的判断,本题考查了转化的思想分类讨论思想等,由于本题运算量较大,易因运算导致错误,解题时要严谨

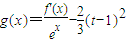 ,求函数g(x)在区间(-2,t)内的零点个数.
,求函数g(x)在区间(-2,t)内的零点个数.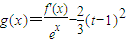 的解析式,由所得的解析式,及零点判定定理知,可研究此函数在区间(-2,t)两个端点值的符号及区间内函数最值的符号,由定理判断出零点个数即可
的解析式,由所得的解析式,及零点判定定理知,可研究此函数在区间(-2,t)两个端点值的符号及区间内函数最值的符号,由定理判断出零点个数即可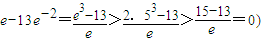 ,
,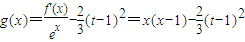
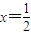 的抛物线,
的抛物线,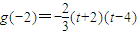 ,
,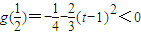 ,
,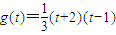 .
.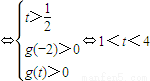 ;…(9分)
;…(9分)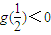 可知,函数g(x)在区间(-2,t)内只有一个零点;…(11分)
可知,函数g(x)在区间(-2,t)内只有一个零点;…(11分)
