
 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
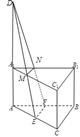
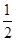 AC=1,∴DE=2∵EF=
AC=1,∴DE=2∵EF=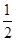
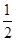 ×2×1=1,∵DA=6
×2×1=1,∵DA=6 ,∴DA1=
,∴DA1=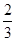 DA∴SDMN=
DA∴SDMN=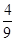 S△DEF=
S△DEF=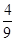 ,∴截面的面积为1
,∴截面的面积为1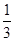
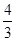 ∴射影EFPQ的面积为
∴射影EFPQ的面积为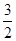 ,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为
,∵截面与平面ABC所成的二面角的大小为60°,∴截面EFN'M'的面积为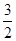 ÷cos60°=3故答案为A
÷cos60°=3故答案为A

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
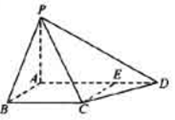
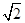 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,对角线
中,对角线 于
于 ,
, ,
, 为
为 的重心,过点
的重心,过点 的直线
的直线 分别交
分别交 于
于 且
且 ‖
‖ ,沿
,沿 将
将 折起,沿
折起,沿 将
将 折起,
折起, 正好重合于
正好重合于 .
. 
 平面
平面 ;
;  与平面
与平面 夹角的大小.
夹角的大小. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题: ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ;
; ,
, ,
, ,则
,则 ;④ 若
;④ 若 ,
, ,
, ,则
,则 .
.| A.①④ | B.①③ | C.②③④ | D.②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com