
 .
. ,求f(α)的值.
,求f(α)的值.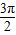 -α变为为π+
-α变为为π+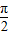 -α,利用诱导公式变形,第三个因式利用诱导公式变形,分母第一个因式根据正切函数为奇函数化简,然后利用诱导公式变形,第二个因式先利用正弦函数为奇函数,再把角3π-α变形为2π+π-α,利用诱导公式变形,约分后即可得到最简结果;
-α,利用诱导公式变形,第三个因式利用诱导公式变形,分母第一个因式根据正切函数为奇函数化简,然后利用诱导公式变形,第二个因式先利用正弦函数为奇函数,再把角3π-α变形为2π+π-α,利用诱导公式变形,约分后即可得到最简结果;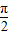 -α),利用诱导公式及正切函数为奇函数化简,得到tan(
-α),利用诱导公式及正切函数为奇函数化简,得到tan(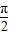 -α)的值,再利用同角三角函数间的基本关系弦化切,并利用诱导公式化简,得到sinα和cosα的关系式,记作①,同时得到sinα和cosα同号,即α为第一或第三象限的角,根据同角三角函数间的平方关系得到sin2α+cos2α=1,记作②,联立①②,求出cosα的值,代入化简后的f(α)的式子中,即可求出f(α)的值.
-α)的值,再利用同角三角函数间的基本关系弦化切,并利用诱导公式化简,得到sinα和cosα的关系式,记作①,同时得到sinα和cosα同号,即α为第一或第三象限的角,根据同角三角函数间的平方关系得到sin2α+cos2α=1,记作②,联立①②,求出cosα的值,代入化简后的f(α)的式子中,即可求出f(α)的值. …(2分)
…(2分)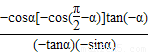
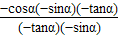
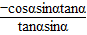
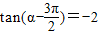 ,
,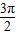 -α)=-tan(
-α)=-tan(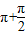 -α)=-tan(
-α)=-tan( -α)=-2,
-α)=-2,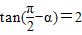 ,
,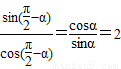 ,
,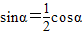 ①,…(6分)
①,…(6分)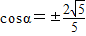 ,
,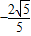 ;…(10分)
;…(10分) .…(12分)
.…(12分)

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com