
分析 (Ⅰ)问题转化为$t≤{[(a-c)•(\frac{1}{a-b}+\frac{1}{b-c})]_{min}}$,利用基本不等式的性质求出即可;
(Ⅱ)问题转化为?n∈R,$|{n+sinγ}|-|{n-cosγ}|≥\sqrt{2}$”是真命题,根据三角函数以及绝对值的意义求出n的范围即可.
解答 解:(Ⅰ)因为“?a>b>c,$\frac{1}{a-b}+\frac{1}{b-c}≥\frac{t}{a-c}$”是真命题,
所以?a>b>c,$\frac{1}{a-b}+\frac{1}{b-c}≥\frac{t}{a-c}$恒成立,
又a>b>c,所以$t≤(a-c)•(\frac{1}{a-b}+\frac{1}{b-c})$恒成立,
所以,$t≤{[(a-c)•(\frac{1}{a-b}+\frac{1}{b-c})]_{min}}$.…(3分)
又因为$(a-c)•(\frac{1}{a-b}+\frac{1}{b-c})=(a-b+b-c)•(\frac{1}{a-b}+\frac{1}{b-c})$=$2+\frac{b-c}{a-b}+\frac{a-b}{b-c}≥4$,
“=”成立当且仅当b-c=a-b时.
因此,t≤4,于是m=4.…(5分)
(Ⅱ)由(Ⅰ)得,因为“?n∈R,$|{n+sinγ}|-|{n-cosγ}|<{m^{\frac{1}{4}}}$”是假命题,
所以“?n∈R,$|{n+sinγ}|-|{n-cosγ}|≥\sqrt{2}$”是真命题.…(7分)
因为|n+sinγ|-|n-cosγ|=|n+sinγ|-|cosγ-n|≤|sinγ+cosγ|$≤\sqrt{2}$($γ∈(0,\frac{π}{2})$),
因此,$|{n+sinγ}|-|{n-cosγ}|=\sqrt{2}$,此时$|{sinγ+cosγ}|=\sqrt{2}$,即$γ=\frac{π}{4}$时.…(8分)
∴$|{n+\frac{{\sqrt{2}}}{2}}|-|{n-\frac{{\sqrt{2}}}{2}}|=\sqrt{2}$,
由绝对值的意义可知,$n≥\frac{{\sqrt{2}}}{2}$.…(10分)
点评 本题考察了基本不等式的性质,考察三角函数问题以及绝对值的意义,考察转化思想,是一道中档题.


科目:高中数学 来源: 题型:填空题
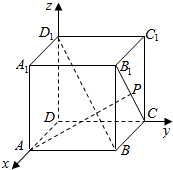 如图所示,正方体ABCD-A1B1C1D1的棱长为1,以D为原点,以正方体的三条棱DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,若点P在正方体的侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则下列点P的坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)中正确的是①②⑤.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,以D为原点,以正方体的三条棱DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,若点P在正方体的侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则下列点P的坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)中正确的是①②⑤.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | $\sqrt{11}$-1 | C. | $\sqrt{3}$+1 | D. | $\sqrt{11}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
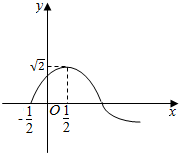 若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )
若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )| A. | 0 | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com